- •Класификация видов движения подвижных сред и методы описания движения жидкости (методы Эйлера и Лагранжа)
- •Кинематика жидкости. Основные понятия (линия тока, элементарная струйка) и определения (живое сечение струйки, смоченный периметр).
- •Поток и его характеристики: геометрич, кинематич, и режимные
- •Уравнение неразрывности для элементарной струйки и потока реальной жидкости. Понятия массового и объемного расхода.
- •Вывод дифер. Уравнений движения идеальной жидкости (уравнений Эйлера).
- •Уравнение Бернули для потока реальной жид. И его геометрич. И энергетич. Представление. Корректив кинетич. Энергии потока. Коэф. Кориолиса.
- •Диф. Ур. Движения реальных жид. (уравнение Новье-Стокса). Критери гидродинамического подобия
- •Опоты Рейнольдса. Критерии Рейнольдса. Ламин., турб, переходной режимы
- •Расчет расхода жидкости при ламинарном режиме ( уравнение Пуазеля)
- •Течение жидкости в малом зазоре. Уравнение Петрова.
- •Понятие местного сопротивления. Основные их виды. Расчет потерь напора на их преодоление. Эквивалентная длинна местных сопротивлений.
- •Внезапное расширение потока. Расчет потерь напора (уравнение Борда)
- •Простой трубопровод. Расчет потерь напора в трубопроводе. Кривые потребного напора простого трубопровода.
- •Понятие гидравлического удара. Формула Журавского. Определение величины повышения давления при прямом полном и неполном гидравлическом ударе.
- •Истечение жидкости через отверстие в тонкой стенке при постоянном напоре.
- •Истечение жидкости через насадок. Определение глубины вакуума в насадке.
- •28, 29, 30) Основная классификация гидромашин по силовому воздействию на жидкость. Насосы. Классификация насосов. Отличительные особенности насосов объёмного и динамического типов.
- •31) Основные технические показатели насосов.
- •3 2,33) Графические характеристики центробежных насосов. Главная характеристика насоса. Рабочая область насоса.
- •34) Устройство и принцип действия центробежного насоса. Трансформация д. Бернули в центробежном насосе. Запуск насоса в работу.
- •36) Основное уравнение центробежных машин. Теоретический и действительные напоры центробежного насоса.
- •37) Совместная работа насоса и трубопровода. Глубина всасывания насоса.
- •38)Насосная установка. Определение напора развиваемого насосом.
- •40) Работа насоса на сеть. Определение положения рабочей точки насоса.
- •41) Подбор центробежного насоса по каталогам. Методика подбора насоса для простого трубопровода.
- •43) Регулирование подачи центробежного насоса изменением характеристики сети. Другие методы регулирования подачи насоса и их анализ.
- •44) Регулирование подачи насоса изменений главной характеристикой насоса. Достоинства и недостатки главного метода.
- •45)Последовательное включение насосов в насосной установке. Построение результирующей характеристики установки и определение её рабочей точки.
- •46) Паралельное включение насосов в насосной установке. Построение результирующей характеристики установки и определение её рабочей точки.
- •47) Явление кавитации в насосных установках. Кавитационный запас. Уравнение Руднёва.
- •48) Шестерённые насосы. Устройство и принцип действия, главная характеристика.
- •49) Определение производительности шестерённого насоса. Методы регулирования подачи насоса.
- •50) Устройство и область применения и принцип работы инжектора. Определение коэффициента инжекции.
34) Устройство и принцип действия центробежного насоса. Трансформация д. Бернули в центробежном насосе. Запуск насоса в работу.
Работа любого насоса и, в частности, центробежного основывается на двух физических свойствах жидкости: вязкости и липкости (свойство адгезии). В центробежном насосе перемещение жидкости осуществляется под действием центробежных сил от центра рабочего колеса к его периферии. При этом в центре образуется разряжение, благодаря которому за счет атмосферного давления в насос поступают новые порции жидкости.
При
вращении рабочего колеса жидкость
участвует в двух видах движения:
переносном (совместно с рабочим колесом
относительно оси вращения) со скоростью
ω1
– в начале лопатки и ω2
– на сходе с нее и относительном (вдоль
лопатки колеса от центра к периферии)
с соответствующими скоростями U1
и U2.
Результирующая или абсолютная скорость
жидкости ( 1
– на входе в колесо и
2
– на выходе из него) определяется как
геометрическая сумма соответствующих
скоростей, а именно:
1
– на входе в колесо и
2
– на выходе из него) определяется как
геометрическая сумма соответствующих
скоростей, а именно:
 и
и  .
После схода жидкости с кромки рабочего
колеса она перемещается в постоянно
расширяющемся зазоре между корпусом 1
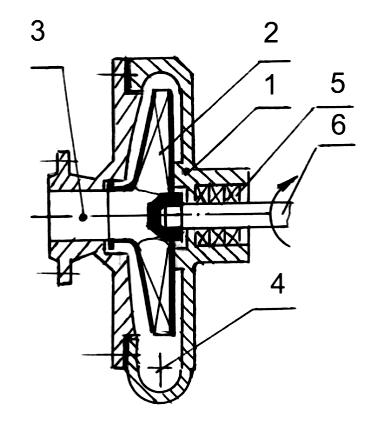
и рабочим колесом 2 насоса (рис.).
.
После схода жидкости с кромки рабочего
колеса она перемещается в постоянно
расширяющемся зазоре между корпусом 1
и рабочим колесом 2 насоса (рис.).
|
|
1 – корпус насоса; 2 – рабочее колесо; 3 – входной патрубок насоса; 4 – выходной (нагнетательный) патрубок; 5 – сальниковое уплотнение; 6 – вал привода
Выделив сечения 1 – 1 и 2 – 2, объединим их уравнением Бернулли

Будем считать, что расстояние между выделенными сечениями вдоль корпуса незначительно, поэтому величину гидравлических потерь Σhп можем приравнять нулю. Учитывая, что сечения 1 – 1 и 2 – 2 расположены достаточно близко, то разностью их геометрических высот расположения Z1 – Z2 можем пренебречь. В результате принятых допущений уравнение Бернулли примет вид

Зная,
что зазор, в котором движется жидкость,
постоянно увеличивающийся, в направлении
выхода из насоса будет справедливо
соотношение S1<S2
и
приняв во внимание уравнение неразрывности
потока.
приходим
к выводу об изменении скорости движения
жидкости в рассматриваемых сечениях
от значения υ1
(в сечении 1 – 1) до значения υ2
(в сечении 2 – 2). При этом меняется и
удельная кинетическая энергия потока
(скоростной напор )
от  до
до
 .
Таким образом, справедливо утверждение
о том, что
.
Таким образом, справедливо утверждение
о том, что
 Однако
для сохранения справедливости равенства
(11.18) необходимо, чтобы статическое
давление в соответствующих сечениях
было обратно т.е.
Однако
для сохранения справедливости равенства
(11.18) необходимо, чтобы статическое
давление в соответствующих сечениях
было обратно т.е.
 Это
означает, что при перемещении жидкости
вдоль корпуса насоса его кинетическая
энергия уменьшается, а потенциальная
возрастает, тем самым на выходе из насоса
жидкость будет обладает большим
статическим напором, нежели на входе.
Взаимный переход одного вида энергии
в другой и обратно называется
«трансформацией Бернулли».
Это
означает, что при перемещении жидкости
вдоль корпуса насоса его кинетическая
энергия уменьшается, а потенциальная
возрастает, тем самым на выходе из насоса
жидкость будет обладает большим
статическим напором, нежели на входе.
Взаимный переход одного вида энергии
в другой и обратно называется
«трансформацией Бернулли».
Чтобы запустить насос, надо в центральной области запустить разряжение: заливка жидкости, установка насоса ниже уровня жидкости, установкой на линии всасывания устройств, предотвращающих сток жидкости при откл. насоса. таким устройством является обратный клапан.
35) Движение жидкости в канале рабочего колеса насоса. Определение расхода жидкости.Движение реальной жидкости в межлопаточных каналах рабочего колеса представляет собой весьма сложный гидромеханический процесс. Поэтому до настоящего времени уравнения движения получить чисто теоретическим путем не удается. Теоретические уравнения движения жидкости в межлопаточных каналах динамических гидромашин (лопаточных насосов и гидротурбин) получены Л.Эйлером при следующих двух допущениях: 1 Жидкость идеальная, т.е. гидравлические сопротивления не учитываются. 2 Жидкость движется в виде бесконечного числа элементарных струек, строго повторяющих форму лопаток.
 Эти
допущения облегчают теоретическое
исследование движения жидкости в
лопаточных системах, но в дальнейшем
требуют внесения существенных поправок
на основании экспериментальных
исследований. Движение каждой частицы
жидкости потока в рабочем колесе является
сложным, абсолютная скорость, которой
складывается из переносной и относительной
скоростей. Скорость переносного движения
- это линейная скорость вращательного
движения точки рабочего колеса, где в
данный момент находится частица жидкости.
Эта скорость направлена по касательной
к окружности, на которой находится
частица. Относительная скорость - это
скорость перемещения частицы относительно
лопатки колеса: вектор относительной
скорости направлен по касательной к
лопатке.
Подачей
(производительностью) насоса называется
объем жидкости, проходящей в единицу
времени через нагнетательный патрубок
насоса.
Она может измеряться в следующих
единицах: м3/с;
м3/ч;
л/с; л/мин (1 л/с ≈ 10-3
м3/с).
Зная u2,
скорость относительного движения частиц
жидкости на выходе из рабочего колеса
(см. рис.), возможно определить его подачу,
применив уравнение объёмного секундного
расхода:
Эти
допущения облегчают теоретическое
исследование движения жидкости в
лопаточных системах, но в дальнейшем
требуют внесения существенных поправок
на основании экспериментальных
исследований. Движение каждой частицы
жидкости потока в рабочем колесе является
сложным, абсолютная скорость, которой
складывается из переносной и относительной
скоростей. Скорость переносного движения
- это линейная скорость вращательного
движения точки рабочего колеса, где в
данный момент находится частица жидкости.
Эта скорость направлена по касательной
к окружности, на которой находится
частица. Относительная скорость - это
скорость перемещения частицы относительно
лопатки колеса: вектор относительной
скорости направлен по касательной к
лопатке.
Подачей
(производительностью) насоса называется
объем жидкости, проходящей в единицу
времени через нагнетательный патрубок
насоса.
Она может измеряться в следующих
единицах: м3/с;
м3/ч;
л/с; л/мин (1 л/с ≈ 10-3
м3/с).
Зная u2,
скорость относительного движения частиц
жидкости на выходе из рабочего колеса
(см. рис.), возможно определить его подачу,
применив уравнение объёмного секундного
расхода:

где
f
– площадь
сечения потока, сходящего с рабочего
колеса насоса,


здесь
 –
высота канала, м.L
− длина пути схода жидкости с рабочего
колеса насоса (длина свободного периметра
рабочего колеса насоса):
–
высота канала, м.L
− длина пути схода жидкости с рабочего
колеса насоса (длина свободного периметра
рабочего колеса насоса):

где
 и
и  – толщина и количество лопастей в
рабочем колесе.
– толщина и количество лопастей в
рабочем колесе.
С учетом уравнений (11.11) и (11.12) подача центробежного насоса составит

 здесь
ψ – коэффициент сжатия лопастями
периметра рабочего колеса насоса:
здесь
ψ – коэффициент сжатия лопастями
периметра рабочего колеса насоса: