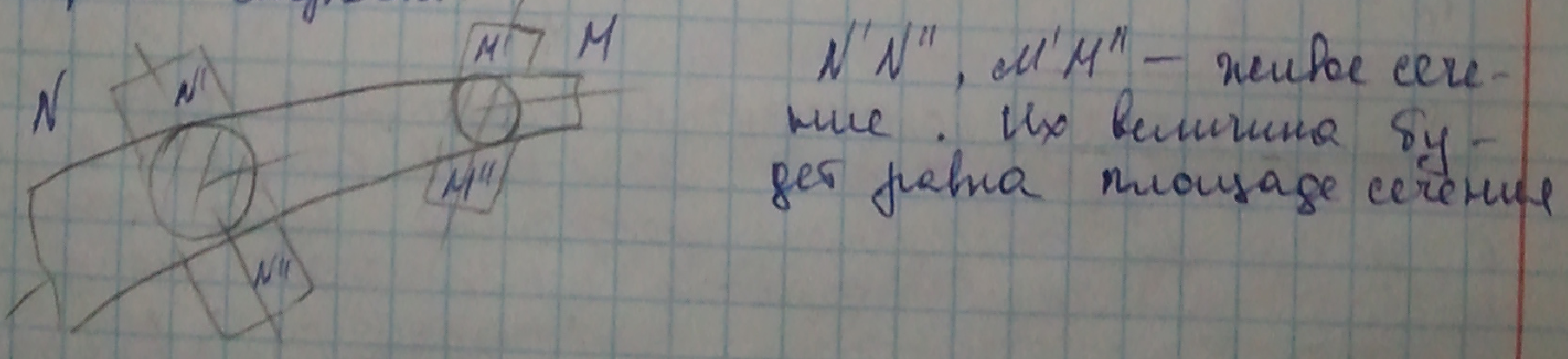- •Класификация видов движения подвижных сред и методы описания движения жидкости (методы Эйлера и Лагранжа)
- •Кинематика жидкости. Основные понятия (линия тока, элементарная струйка) и определения (живое сечение струйки, смоченный периметр).
- •Поток и его характеристики: геометрич, кинематич, и режимные
- •Уравнение неразрывности для элементарной струйки и потока реальной жидкости. Понятия массового и объемного расхода.
- •Вывод дифер. Уравнений движения идеальной жидкости (уравнений Эйлера).
- •Уравнение Бернули для потока реальной жид. И его геометрич. И энергетич. Представление. Корректив кинетич. Энергии потока. Коэф. Кориолиса.
- •Диф. Ур. Движения реальных жид. (уравнение Новье-Стокса). Критери гидродинамического подобия
- •Опоты Рейнольдса. Критерии Рейнольдса. Ламин., турб, переходной режимы
- •Расчет расхода жидкости при ламинарном режиме ( уравнение Пуазеля)
- •Течение жидкости в малом зазоре. Уравнение Петрова.
- •Понятие местного сопротивления. Основные их виды. Расчет потерь напора на их преодоление. Эквивалентная длинна местных сопротивлений.
- •Внезапное расширение потока. Расчет потерь напора (уравнение Борда)
- •Простой трубопровод. Расчет потерь напора в трубопроводе. Кривые потребного напора простого трубопровода.
- •Понятие гидравлического удара. Формула Журавского. Определение величины повышения давления при прямом полном и неполном гидравлическом ударе.
- •Истечение жидкости через отверстие в тонкой стенке при постоянном напоре.
- •Истечение жидкости через насадок. Определение глубины вакуума в насадке.
- •28, 29, 30) Основная классификация гидромашин по силовому воздействию на жидкость. Насосы. Классификация насосов. Отличительные особенности насосов объёмного и динамического типов.
- •31) Основные технические показатели насосов.
- •3 2,33) Графические характеристики центробежных насосов. Главная характеристика насоса. Рабочая область насоса.
- •34) Устройство и принцип действия центробежного насоса. Трансформация д. Бернули в центробежном насосе. Запуск насоса в работу.
- •36) Основное уравнение центробежных машин. Теоретический и действительные напоры центробежного насоса.
- •37) Совместная работа насоса и трубопровода. Глубина всасывания насоса.
- •38)Насосная установка. Определение напора развиваемого насосом.
- •40) Работа насоса на сеть. Определение положения рабочей точки насоса.
- •41) Подбор центробежного насоса по каталогам. Методика подбора насоса для простого трубопровода.
- •43) Регулирование подачи центробежного насоса изменением характеристики сети. Другие методы регулирования подачи насоса и их анализ.
- •44) Регулирование подачи насоса изменений главной характеристикой насоса. Достоинства и недостатки главного метода.
- •45)Последовательное включение насосов в насосной установке. Построение результирующей характеристики установки и определение её рабочей точки.
- •46) Паралельное включение насосов в насосной установке. Построение результирующей характеристики установки и определение её рабочей точки.
- •47) Явление кавитации в насосных установках. Кавитационный запас. Уравнение Руднёва.
- •48) Шестерённые насосы. Устройство и принцип действия, главная характеристика.
- •49) Определение производительности шестерённого насоса. Методы регулирования подачи насоса.
- •50) Устройство и область применения и принцип работы инжектора. Определение коэффициента инжекции.
Класификация видов движения подвижных сред и методы описания движения жидкости (методы Эйлера и Лагранжа)
Движение
жидкости, по сравнению с движением
твёрдого тела, отличается большей
сложностью. Если состояние жидкости в
покое характеризовалось лишь
гидростатическим давлением, то в движении
её состояние характеризуется наравне
с давлением ещё и скоростью частиц
жидкости. В общем случае значение
давления и скорости, различные в различных
точках пространства, могут изменяться
также и во времени. Если скорость и
давление в каждой точке пространства,
заполненного движущейся жидкостью,
остаётся во времени постоянным (но могут
меняться при переходе от одной точки
пространства к другой), движение
называется установившимся. Это движение
постоянное во времени, изменяющееся в
пространстве.
В этом случае скорость и давление зависит
от координат движущейся жидкой частицы.
Например, истечение жидкости через
отверстие в баке с постоянным уровнем.
Описывается оно системой уравнений:
 ;
; ;
; .
При неустановившемся движении жидкости
поле скоростей и поле давлений будет
непрерывно изменяться и зависеть как
от координат движущейся частицы, так и
от времени. Примером неустановившегося
движения является истечение жидкости
через отверстие в стенке бака с переменным
уровнем и описывается системой уравнений:
.
При неустановившемся движении жидкости
поле скоростей и поле давлений будет
непрерывно изменяться и зависеть как
от координат движущейся частицы, так и
от времени. Примером неустановившегося
движения является истечение жидкости
через отверстие в стенке бака с переменным
уровнем и описывается системой уравнений:
 ;
; ;
;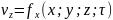 .
Различают также равномерное и неравномерное
движение. При равномерном движении
жидкости поле скоростей остаётся
постоянным во времени вдоль одной из
координатных осей. Основу
описания движения точки в гидравлике
положен метод Эйлера.
Согласно кот. расм. изменение скорости
движения жидкой частицы проходящей
через неподвижную точку пространства.
Таким образом по гипотезе Эйлера поток
в целом в данный момент времени представлен
векторным полем скоростей. В данном
случае скорость будет явл. функцией
координат и времени. Метод
Лагранжа:
В потоке жидкости в целом судят по
совокупному рассмотрению траектории
движения частиц. Для определения скорости
испол. понятие перемещения частиц взятое
за бесконечно малый промежуток времени,
при этом длинна перемещения представляет
собой расстояние между двумя точками
взятыми на траекторию с учетом того что
траектория проходит через заданую точку
пространства. Это перемещение или путь
за бесконечно малый промежуток времени
обозначаеться через ds,dl,dτ.
.
Различают также равномерное и неравномерное
движение. При равномерном движении
жидкости поле скоростей остаётся
постоянным во времени вдоль одной из
координатных осей. Основу
описания движения точки в гидравлике
положен метод Эйлера.
Согласно кот. расм. изменение скорости
движения жидкой частицы проходящей
через неподвижную точку пространства.
Таким образом по гипотезе Эйлера поток
в целом в данный момент времени представлен
векторным полем скоростей. В данном
случае скорость будет явл. функцией
координат и времени. Метод
Лагранжа:
В потоке жидкости в целом судят по
совокупному рассмотрению траектории
движения частиц. Для определения скорости
испол. понятие перемещения частиц взятое
за бесконечно малый промежуток времени,
при этом длинна перемещения представляет
собой расстояние между двумя точками
взятыми на траекторию с учетом того что
траектория проходит через заданую точку
пространства. Это перемещение или путь
за бесконечно малый промежуток времени
обозначаеться через ds,dl,dτ.


Кинематика жидкости. Основные понятия (линия тока, элементарная струйка) и определения (живое сечение струйки, смоченный периметр).
К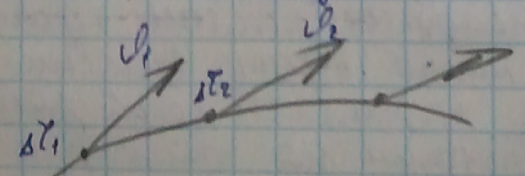


 инематикой
жидкости наз раздел в мжиг в котором
движение частиц подвижных сред изучается
вне зависимости от действия внешних
сил. В кинематике устанавливают связь
между геометрич. хара-ми потока и
временем. Причинами движения жидкости
явл. силы действующие в жид-ти массовые
или объемные и поверхностные силы, силы
давления и трения. В отличии от
гидростатики, где основной характеристикой
явл. давление кот. определяеться от
координат, в гидродинамике рассм. их
скорость. Движение частиц характеризуется
скоростью. В каждый момент времени
частица имеет свою скорость по направлению
и величине. Если проследить движение
частицы за достаточноо большой промежуток
времени, то можно получить геометрич.
место точек этой частицы в пространстве
за время. Это ГМТ будет представлять
собой траекторию движения частицы. Если
каждой частице в каждый промежуток
времени движущейся по своей траектории
выделить точку и указать вектор скорости
ν1τ1, след. промежуток ν2τ2 и т.д. и к этим
векторам провести касательную линию,
то получаем линию, к-ая наз. линией
тока жидкости.
Главная особенность линии тока явл. то
что частицы ее не пересекают. Замкнутое
пространство образованное совокупностью
линий тока наз.
трубкой тока.
Т.е поверхность образована линиями
тока, то переход частиц изнутри трубки
тока через ее повер-ть не происходит.
Жидкость нах. внутри трубки тока,
ограниченную поверхностью трубки тока
наз.
элементарной струйкой. Смоченным
периметром
наз. сумму длин сторон стенок ограничивающих
поток и контактирующие с ним. Обозначаеться
инематикой
жидкости наз раздел в мжиг в котором
движение частиц подвижных сред изучается
вне зависимости от действия внешних
сил. В кинематике устанавливают связь
между геометрич. хара-ми потока и
временем. Причинами движения жидкости
явл. силы действующие в жид-ти массовые
или объемные и поверхностные силы, силы
давления и трения. В отличии от
гидростатики, где основной характеристикой
явл. давление кот. определяеться от
координат, в гидродинамике рассм. их
скорость. Движение частиц характеризуется
скоростью. В каждый момент времени
частица имеет свою скорость по направлению
и величине. Если проследить движение
частицы за достаточноо большой промежуток
времени, то можно получить геометрич.
место точек этой частицы в пространстве
за время. Это ГМТ будет представлять
собой траекторию движения частицы. Если
каждой частице в каждый промежуток
времени движущейся по своей траектории
выделить точку и указать вектор скорости
ν1τ1, след. промежуток ν2τ2 и т.д. и к этим
векторам провести касательную линию,
то получаем линию, к-ая наз. линией
тока жидкости.
Главная особенность линии тока явл. то
что частицы ее не пересекают. Замкнутое
пространство образованное совокупностью
линий тока наз.
трубкой тока.
Т.е поверхность образована линиями
тока, то переход частиц изнутри трубки
тока через ее повер-ть не происходит.
Жидкость нах. внутри трубки тока,
ограниченную поверхностью трубки тока
наз.
элементарной струйкой. Смоченным
периметром
наз. сумму длин сторон стенок ограничивающих
поток и контактирующие с ним. Обозначаеться
 .
Если же поток не полностью заполняет
сечение, то смоченым периметром будет
явл. длинна стенок. Измеряется в метрах.
Живым
сечением потока
наз. площадь сечения потока полученная
секущей плоскостью перпендикул.
расположеной к векторам скорости.
Величина этих сечений будет равна
площади живого сечения потока. Однако
движение жидкости можно представить
как паралельные струйки с малым углом
отклонения.
.
Если же поток не полностью заполняет
сечение, то смоченым периметром будет
явл. длинна стенок. Измеряется в метрах.
Живым
сечением потока
наз. площадь сечения потока полученная
секущей плоскостью перпендикул.
расположеной к векторам скорости.
Величина этих сечений будет равна
площади живого сечения потока. Однако
движение жидкости можно представить
как паралельные струйки с малым углом
отклонения.