21.Определение вектора, противоположного вектора, длины вектора, нулевого и единичного векторов, коллинеарных. Равных и компланарных векторов.

Вектор – направленный отрезок, то есть отрезок, имеющий длину и направление.

Вектор, противоположный вектору 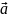, называется .

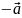Длиной или модулем вектора 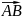называется длина отрезка и обозначается .

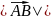Вектор, длина которого равна нуля, называется нулевым вектором и обозначается 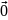. Нулевой вектор не имеет направления.

Вектор, длина которого равна единице, называется единичным и обозн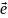ачается . Единичный вектор, направление которого совпадает с направлением вектора , называется орта вектора и обозначается .

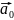Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обознач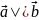аются . Коллинеарные векторы могут быть направлены одинаково (сонаправлены) и обозначаются 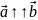и противоположно направлены - .

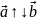2 вектора называются равными, если они одинаково направлены и имеют одинаковые длины.

Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

22.Линейные операции над векторами.

1. Сумма векторов – это вектор, который можно найти по правилу треугольника или правилу параллелограмма. 3 вектора, не принадлежащие одной плоскости, можно найти по правилу параллелепипеда.

2. Разностью векторов и 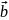называют вектор 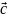, равный 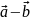, такой, что вектор .

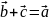3. Произведением вектора на число α называется вектор 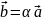имеющий длину 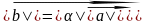, направление которого совпадает с направлением вектора , если 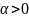, и противоположно ему, если .

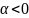Из определения произведения векторов следует, что

1. если и 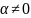, то и коллинеарные, и наоборот, если векторы и – коллинеарные (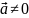 ), при некотором α верно равенство .

2. Если 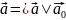, то это означает, что каждый вектор равен произведению его модуля на орт.

Свойства линейных операций над векторами:

1. a+b=b+a

2. a+(b+c)=(a+b)+с

3. α(a+b)=αa+αb

4. (α+β)a=αa+βa

5. (αβ)a=α(βa)

6. a+0=a

7. Для любого вектора a существует противоположный ему вектор, такой, что –a, то есть a+(-a)=0.

8. 0a=0

9. 1a=a

23.Формула разложения вектора по ортам координатных осей. Координаты вектора. Выражение линейных операций над векторами в координатах.

Проекцией вектора на ось называется положительное число, если вектор и ось одинаково направлены, и отрицательное число, если вектор и ось противоположно направлены.

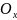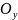– ось абсцисс, – ось ординат, 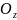– ось аппликат; - называются осями координат, взаимно перпендикулярны.

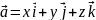- Формула разложения вектора по ортам координатных осей.

Числа x, y, z называются координатами , то есть координаты вектора есть проекции на соответствующие координатные оси. Если вектор имеет начало в начале координат, то его координатами называют числа, являющиеся координатами его конца. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно записать, что модуль вектора равен сумме квадратов его проекций на оси.

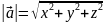– длина вектора.

Выражение линейных операций над векторами в координатах:

1. Суммой векторов называется вектор равный сумме соответствующих координат, складывающихся векторов.

Произведением векторов на число является произведение числа на соответствующие координаты.

Векторы называются равными, если их координаты равны.

Векторы называются коллинеарными, если их координаты пропорциональны.

Чтобы найти координаты вектора, нужно от координат его конца отнять координаты его начала.