
- •2. Определение матриц. Виды матриц.
- •1. Математическая модель. Этапы математического моделирования.
- •3. Транспонирование матриц. Свойства.
- •5. Произведение матриц. Возведение матриц в степень. Свойства произведения.
- •6. Вычисление определителей 2-го и 3-го порядков. Свойства определителей.
- •7. Минор и их алгебраическое дополнение элемента матрицы.
- •8. Вычисление определителей n-го порядка разложением по ряду и приведением к треугольному виду.
- •9. Определение обратной матрицы. Условие существования обратной матрицы. Формула нахождения обратной матрицы.
- •11. (Только практика) Способы вычисления ранга.
- •12.Сформулировать элементарные преобразования матриц. Определение эквивалентных матриц.
- •15.(Только практика) Решение системы матричным способом.
- •16.(Только практика) Решение системы методом Крамера.
- •17.(Только практика) Решение системы методом Гаусса.
- •18.Совместная и несовместная система. Критерий совместности системы. Правила практического разыскания решений.
- •19.(Только практика) Алгоритм решения произвольной системы линейных уравнений.
- •20.Определение однородной системы уравнений. Сформулировать теорему об условии существования нетривиального решения. Что называется фундаментальной системой решения?
- •21.Определение вектора, противоположного вектора, длины вектора, нулевого и единичного векторов, коллинеарных. Равных и компланарных векторов.
- •22.Линейные операции над векторами.
- •23.Формула разложения вектора по ортам координатных осей. Координаты вектора. Выражение линейных операций над векторами в координатах.
- •24.Формула деления отрезка в заданном отношении.
- •25.Определение скалярного произведения векторов. Выражение скалярного произведения через координаты.
- •26. Как найти угол между векторами?
- •27.Определение n-мерного вектора и его координат. Определение векторного пространства. Как найти сумму, произведение на число, скалярное произведение и длину n-мерных векторов?
- •28.Линейная комбинация векторов. Определение линейно зависимой и независимой системы.
- •29.Уравнения прямой на плоскости (6 видов).
- •30.Угол между прямыми и условия параллельности и перпендикулярности двух прямых.
- •31.Расстояние от точки до прямой.
- •32.Уравнения плоскости в пространстве (4 вида).
- •33.Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
- •34.Расстояние от точки до плоскости.
- •35.Уравнения прямой в пространстве (4 вида)
- •40.Определение гиперболы и се каноническое уравнение. Исследование формы гиперболы. Асимптоты гиперболы. Дополнительные сведения о гиперболе.
- •41.Парабола и ее каноническое уравнение. Исследование формы параболы.
- •43.Определение предела последовательности и его геометрическая интерпретация.
- •44.Свойства сходящихся последовательностей.
- •45.Определение, способы задания и свойства функции.
- •46.1)Определение предела функции в точке 2)Предел функции при х→∞ 3)Односторонние пределы.
- •47.Бесконечно малые и бесконечно большие функции и их свойства.
- •48.Основные свойства пределов.
- •49.Замечательные пределы (1-й - с доказательством).
- •50.Определение функции непрерывной в точке, в интервале и на отроке. Точки разрыва.
- •51.Определение производной функции в точке. (производная – это скорость).
- •52. Механический, геометрический и экономический смысл производной.
- •53.Таблица производных элементарных функций. Правила вычисления производных.
- •54.Дифференциал функции и его геометрическая интерпретация. Свойства дифференциала.
- •55.Производные и дифференциалы высших порядков.
43.Определение предела последовательности и его геометрическая интерпретация.
Число
a
называется пределом последовательности
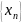 ,
если для любого положительного числа
ϵ
существует такой номер N,
что при всех
,
если для любого положительного числа
ϵ
существует такой номер N,
что при всех
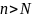 выполняется неравенство
выполняется неравенство
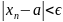 .
В этом случае пишут
.
В этом случае пишут
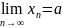 .
Говорят также, что последовательность
сходится к a
или называется сходящейся.
Последовательность, не имеющая предела,
называется расходящейся. Коротко
определение записывают так:
.
Говорят также, что последовательность
сходится к a
или называется сходящейся.
Последовательность, не имеющая предела,
называется расходящейся. Коротко
определение записывают так:
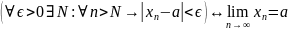 .
.
Геометрическая
интерпретация: заключается в том, что
с увеличением номера члена
последовательности, члены последовательности
приближаются к числу a,
которое является пределом. И поскольку
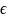 окрестность достаточно маленькая, то
на числовой прямой находится бесконечное
число точек – элементов этой
последовательности, близко расположенных
к a.
окрестность достаточно маленькая, то
на числовой прямой находится бесконечное
число точек – элементов этой
последовательности, близко расположенных
к a.
Неограниченная
последовательность не имеет конечного
предела. Однако она может иметь
бесконечный предел, что записывается
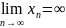 .
Если при этом начиная с некоторого
номера все члены последовательности
положительны (отрицательны), то пишут
.
Если при этом начиная с некоторого
номера все члены последовательности
положительны (отрицательны), то пишут
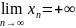 (
(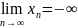 ).
Саму последовательность называют
бесконечно большой. Последовательность,
имеющая своим пределом 0, называют
бесконечно малой.
).
Саму последовательность называют
бесконечно большой. Последовательность,
имеющая своим пределом 0, называют
бесконечно малой.
44.Свойства сходящихся последовательностей.
1.
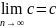
2. Сходящаяся последовательность имеет только 1 предел.
3. Сходящаяся последовательность ограничена.
4.
и
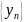 сходятся, то
сходятся, то
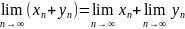 ;
;
 ;
;
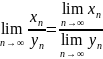
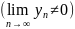 ;
;
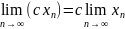 .
.
5. Произведение бмп и ограниченной последовательности или числа есть бмп.
6. Произведение конечного числа бмп-тей и есть бмп.
45.Определение, способы задания и свойства функции.
Если
каждому элементу x
из множества X
по какому-либо закону f
ставится в соответствие единственный
элемент y
из множества Y,
то говорят, что задана функциональная
зависимость y
от x
по закону
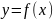 или функция
.
При этом x
называют независимой переменной или
аргументом, y
– зависимой переменной или значением
функции, множество X
называют областью определения функции
и обозначают D(f),
множество Y
– областью значений функции и обозначают
E(f).
или функция
.
При этом x
называют независимой переменной или
аргументом, y
– зависимой переменной или значением
функции, множество X
называют областью определения функции
и обозначают D(f),
множество Y
– областью значений функции и обозначают
E(f).
Основные свойства функции:
1. Четность/нечетность.
Функция
называется четной, если для любого
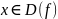 выполняется условия: 1.
выполняется условия: 1.
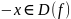 2.
2.
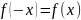 .
И нечетной, если для любого
выполняется условия: 1.
2.
.
И нечетной, если для любого
выполняется условия: 1.
2.
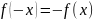 .
При этом
.
При этом
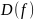 называют симметричной относительно
называют симметричной относительно
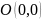 .
График четной функции симметричен
относительно
,
а график нечетной функции относительно
.
.
График четной функции симметричен
относительно
,
а график нечетной функции относительно
.
2.
Монотонность. Функция называется
возрастающей на промежутке
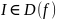 ,
если для любого
,
если для любого
 ,
,
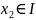 ,
где
,
где
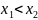 выполняется условие
выполняется условие
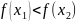 и неубывающей, если
и неубывающей, если
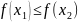 .
Функция называется убывающей на
промежутке
,
если для любого
,
,
где
выполняется условие
.
Функция называется убывающей на
промежутке
,
если для любого
,
,
где
выполняется условие
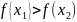 и неубывающей, если
и неубывающей, если
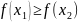 .
Возрастающие, неубывающие, убывающие,
невозрастающие на промежутке
называются монотонными.
.
Возрастающие, неубывающие, убывающие,
невозрастающие на промежутке
называются монотонными.
3.
Ограниченность. Функция называется
ограниченной на множестве
,
если существует M>0
такое, что для всех
выполняется неравенство
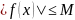 .
.
4.
Периодичность. Функция называется
периодичной на множестве
,
если существует T>0,
что для всех x,
принадлежащих
выполняется условие: 1.
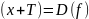 ;
2.
;
2.
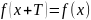 .
T
– период функции. Если T
период, то nT
также является периодом, где
.
T
– период функции. Если T
период, то nT
также является периодом, где
 .
.
