40.Определение гиперболы и се каноническое уравнение. Исследование формы гиперболы. Асимптоты гиперболы. Дополнительные сведения о гиперболе.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до 2ух данных точек этой плоскости, называемой фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. 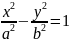– каноническое уравнение гиперболы, где .

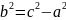Исследование формы гиперболы:

1. Уравнение содержит x и y в четных степенях – гипербола симметрична относительно , и начала координат. Точка – центр гиперболы.

2. Точки пересечения с осью : y=0, , . и – вершины гиперболы. С осью : x=0, 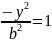– нет точек пересечения с . и . Отрезок 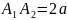– действительная ось. – мнимая ось.

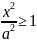
3. 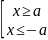– это означает, что точки гиперболы располагаются справа от прямой 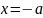и слева от .

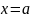Прямая называется асимптотой, если график бесконечно близко приближается к ней, но никогда ее не пересекает. Гипербола имеет 2 асимптоты .

Гипербола называется равносторонней, если a=b. Ее уравнение 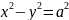. Уравнение равносторонней гиперболы, для которого оси и являются асимптотами, будет иметь вид .

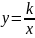Если гипербола определяется уравнением 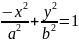, то действительная и мнимая оси меняются местами.

41.Парабола и ее каноническое уравнение. Исследование формы параболы.

Параболой называют множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром p (p>0). .

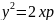Исследование формы параболы:

1. Уравнение в четной степени – парабола симметрична относительно .

2. Так как p>0, то 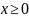. Это значит, парабола расположена справа от .

3. Если x=0, то y=0. Парабола проходит через . Эта точка называется вершиной параболы.

42.Определение числовой последовательности. Ограниченные и монотонные последовательности.

Числовой последовательностью называется множество чисел, все элементы которых пронумерованы всеми натуральными числами. Обозначается:

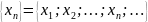
Числа x называются числами последовательности, 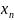– общим или n-ым членом последовательности, n – его номером.

Последовательность задана, если для любого номера n определено правило нахождения элемента последовательности с этим номером. Чаще всего последовательность задают формулой его общего члена.

Последовательность называют ограниченной, если существует такое число M>0, что 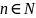выполняется неравенство 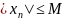. В противном случае последовательность называется неограниченной.

Последовательность называется возрастающей (неубывающей), если для любого n выполняется неравенство 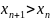( 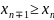). Если каждый последующий член больше предыдущего. Аналогично определяется убывающая (невозрастающая). Все эти последовательности называются монотонными.