32. Кинематические пары и цепи.
Кинематическая цепь — это связанная система объектов, образующих между собой кинематические пары.
Кинематические цепи имеют такую классификацию:
Простые и сложные. В простой кинематической цепи каждое из ее звеньев входит в состав одной или двух кинематических пар, а в сложной кинематической цепи имеются звенья, входящие в состав трех и более кинематических пар.
Открытые и замкнутые. В открытой (незамкнутой) кинематической цепи имеются звенья, входящие в состав одной кинематической пары, а в замкнутой цепи каждое звено входит в состав 2-х и более кинематических пар.
Плоские и пространственные. Если точки всех звеньев кинематической цепи двигаются в одной или параллельных плоскостях, то такая кинематическая цепь называется плоской, в противном случае кинематическая цепь — пространственная, так как точки её звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые.
Кинематическая пара — это соединение двух звеньев, обеспечивающее определённое относительное движение.
Для всех кинематических пар необходим постоянный контакт между их элементами, это достигается либо с помощью определённых усилий, либо придание элементам определённой геометрической формы.
Классификация
По числу связей на относительное движение:
от одного до пяти связей. Это связано со степенями свободы которых как известно, для материального тела шесть, исключая (связывая) по одной мы получаем пять вариантов связей.
По контакту между звеньями:
высшие (контакт по точке или линии);
низшие (контакт по поверхности).
33. Определение эквивалентной нагрузки на шариковые подшипники >>> см. Вопрос 30.
34. Кинематика и геометрия конических зубчатых колес.
В
о
многих машинах осуществление требуемых
движений механизма связано с необходимостью
передать вращение с одного вала на
другой при условии, что оси этих валов
пересекаются. В таких случаях применяют
коническую зубчатую передачу. Различают
виды конических колёс, отличающихся по
форме линий зубьев: с прямыми,
тангенциальными, круговыми и криволинейными
зубьями. Конические колёса с прямым
зубом, например, применяются в автомобильных
дифференциалах, используемых для
передачи момента от двигателя к колёсам.
35. Методы образования эвольвентного профиля зубчатого колеса. Условия появления и устранения подреза ножки зуба.
36. Определение долговечности подшипника в часах.
Долговечность подшипника в часах
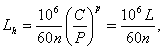(17)
где n — частота вращения подшипника, об/мин. Числовые значения долговечности L в зависимости от отношения и n приведены в табл. Числовые значения Lh можно определить и по уравнению
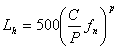(18)
числовые значения fn приведены в табл.
37. Планетарные передачи. Кпд планетарной передачи.
Планетарная передача — механическая система, состоящая из нескольких планетарных зубчатых колёс (шестерён), вращающихся вокруг центральной, солнечной, шестерни. Обычно, планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую шестерню, имеющую внутреннее зацепление с планетарными шестернями.
П. п. имеют высокий кпд (0,96—0,99), но не дают возможности получать большие передаточные отношения