28. Зубчатые механизмы. Виды зубчатых механизмов.

Зубчатый механизм - механизм, в состав которого входят зубчатые звенья.

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов. Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов.

Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами.

Элементы планетарного механизма имеют специальные названия:

• зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";

• колесо с внутренними зубьями называют "короной" или "эпициклом";

• колеса, оси которых подвижны, называют "сателлитами";

• подвижное звено, на котором установлены сателлиты, называют "водилом". Звено водила принято обозначать не цифрой, а латинской буквой h.

29. Задача о положениях.

30. Определение эквивалентной нагрузки на роликовые подшипники.

Прикладываемые к подшипникам нагрузки делятся на радиальные, действующие перпендикулярно центральной оси, и аксиальные, действующие параллельно центральной оси. Эти нагрузки действуют независимо или в сочетании с другими нагрузками. Динамическая эквивалентная нагрузка. Когда к подшипнику одновременно приложены радиальная и аксиальная нагрузки, фактическая нагрузка, действующая на центр подшипника, которая будет определять срок службы, равный определяемому радиальной и аксиальной нагрузками, называется динамической эквивалентной нагрузкой.

31. Динамика механизмов и машин. Основные задачи динамики.

Динамика машин и механизмов, раздел теории машин и механизмов, в котором изучается движение механизмов и машин с учётом действующих на них сил. Д. м. и м. решает следующие основные задачи: установление законов движения звеньев механизмов, регулирование движения звеньев, нахождение потерь на трение, определение реакций в кинематических парах, уравновешивание машин и механизмов.

Определение законов движения звеньев механизма по заданным характеристикам внешних сил решают с помощью дифференциальных уравнений движения механической системы или машинного агрегата, состоящего обычно из двигателя, передаточного механизма, рабочей машины и иногда управляющего устройства. Число уравнений равняется числу степеней свободы этой механической системы. В плоских механизмах с одной степенью свободы для удобства решения задачи все силы и массы приводят к одному звену или точке механизма, которые называются звеном приведения или точкой приведения. Условный момент, приложенный к звену приведения, называется моментом приведения. Момент приведения равен совокупности всех моментов и сил, приложенных к звеньям механизма. Условный момент инерции звена приведения называется приведённым моментом инерции. Кинетическая энергия звена приведения равна сумме кинетических энергий всех звеньев механизма. Аналогично определяют приведённые силу и массу в точке приведения:

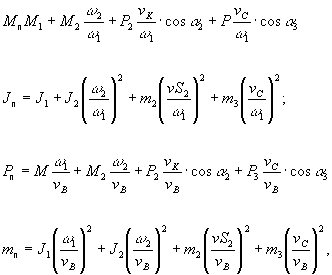
где М_п — приведённый момент; J_п — приведённый момент инерции; Р_п — приведённая сила; m_п — приведённая масса; M₁, M₂, P₂, P₃ — моменты и силы, приложенные к звеньям механизма; w₁, w₂ — угловые скорости звеньев; u_B, u_C — скорости точек В и С механизма; uS₂ — скорость центра тяжести звена 2; u_K — скорость точки К приложения силы P₂; a₂ — угол между векторами P₂ и u_K; a₃ — угол между векторами P₃ и u_C. Уравнение движения для данного случая:

т. е, М_п в общем случае зависит от времени, положения, скорости.