50. Построение механизма по Ассуру. Группа Ассура.

Построение механизмов по Ассуру состоит в последовательном присоединении к ведущим звеньям и стойке особых кинематических цепей называемых структурными группами или группами Ассура без изменения степени подвижности механизма в целом

Группа Ассура - кинематическая цепь с нулевой степенью подвижности относительно тех звеньев к которым она присоединяется своими элементами и которые не распадаются на более простые кинематические цепи с нулевой степенью подвижности

Структурные группы Ассура делятся на классы в зависимости от числа звеньев, образующих группу, числа поводков в группе, числа замкнутых контуров внутри группы. В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков). Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 1-го класса 2-го порядка.

51. Определение числа условий связи.

Вхождение звена в кинематическую пару с другим звеном налагает на относительное движение этих звеньев условиями связи

H=6-S => для того чтобы получить число связей надо посчитать число простейших движений( тут их 5) и вычесть полученное число из количества степеней свободы.

В этом случае число степеней свободы звеньев данной кинематич пары = 5 (H) и число условий связи 1 (S)

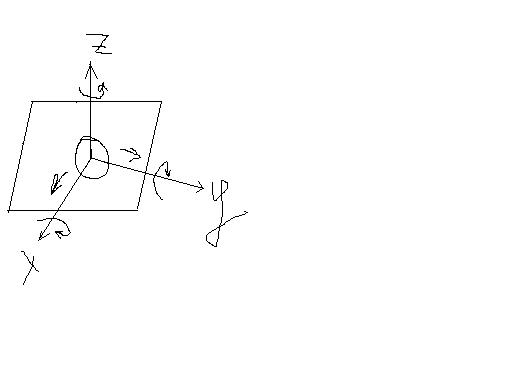
52. Структура плоских механизмов. Формула Чебышева.

W= 3n - 2p5-p4 - формула чебышева

как видно из формулы ,плоские механизмы могут быть образованы звеньями,входящими только в кинематические пары IV и V классов. Пары IV класса в плоских механизмах налагают одно условие связи на относительное движение звеньев, а пары V класса да условия связи. Примером пары IV класса в плоских кинематических цепях может служить пара, образованная звеньями выполненыеми в виде двух цилиндрических поверхностей с паралельными осями, перекатывающихся со скольжением друг по другу и постоянно соприкасающихся по прямолинейным образующим этих поверхностей без скольжения вдоль образующих. Низшие пары V класса (пары в которых касание звеньев происходит по поверхностям) в плоских механизмах являются либо вращательными либо поступательными. Вращательная пара исключает возможность поступательных движений вдоль двух осей, лежащих в плоскости вдижения звеньев. Поступательная пара исключает одно поступателное движение и одно вращательное. Кинематические пары V класса в плоских механизмах могут быть и высшими. Пример может быть таков: две жестко связанные между собой плоские кривые, соприкасающиеся с двумя другими плоскими кривыми, а также жестко связанными между собой. Такие пары получили название двухточечных пар, так как звенья соприкасаются в двух точках.