
- •Особенности геометрии косозубых, шевронных и конических передач
- •1.3. Особенности геометрии конических колес
- •Усилия в зацеплении зубчатых передач
- •1. Расчет зубьев на прочность при изгибе
- •Тема 2. Червячные передачи
- •2.1. Общие сведения. Геометрические и кинематические особенности червячных передач
- •2.2. Усилия в зацеплении. Расчет зубьев колес. Тепловой расчет червячных передач
- •Тепловой расчет и охлаждение червячных передач
- •Общие сведения. Ремни. Шкивы
- •Конструкции ремней и шкивов
- •3.2. Скольжение ремня. Кинематические и геометрические параметры передачи
- •3.3. Усилия и напряжения в ремнях. Тяговая способность и кпд передачи
- •Главные критерии работоспособности передачи
- •Цепные передачи Усилия в элементах передачи. Расчет передачи
- •5.1. Валы и оси. Классификация. Расчет на прочность. Материалы
- •5.2. Опоры валов и осей.
- •5.3. Динамическая грузоподъемность подшипников качения.
- •5.4. Муфты механических приводов.
- •5.5. Муфты общего назначения. Особенности расчета
- •5.6. Предохранительные муфты
- •Тема 6. Соединения деталей и уздов машин
- •6.1. Сварные соединения.
- •6.2. Расчет на прочность и проектирование
- •6.3. Соединения пайкой и склеиванием
- •6.4. Соединения типа "вал - ступица":
- •6.4.1. Шпоночные соединения
- •6.4.2. Шлицевые соединения
- •6.4.3. Профильные соединения
- •6.4.4. Штифтовые соединения
- •6.5. Резьбовые соединения
- •6.5.1. Крепежные детали и стопорящие устройства
- •6.5.2. Резьба и ее параметры
- •6.5.3. Силовые зависимости в резьбовом соединении
- •6.5.5. Расчет резьбовых соединений на прочность
- •6.5.6. Расчет резьбовых соединений
Геометрический расчет эвольвентных прямозубых передач
Рассмотрим
сечение цилиндрического зубчатого
колеса. Выделяют окружность вершин
зубьев (![]() )
и окружность
впадин (
)
и окружность
впадин (![]() ),
между которыми заключен зуб колеса.
Высота зуба
),
между которыми заключен зуб колеса.
Высота зуба
![]()
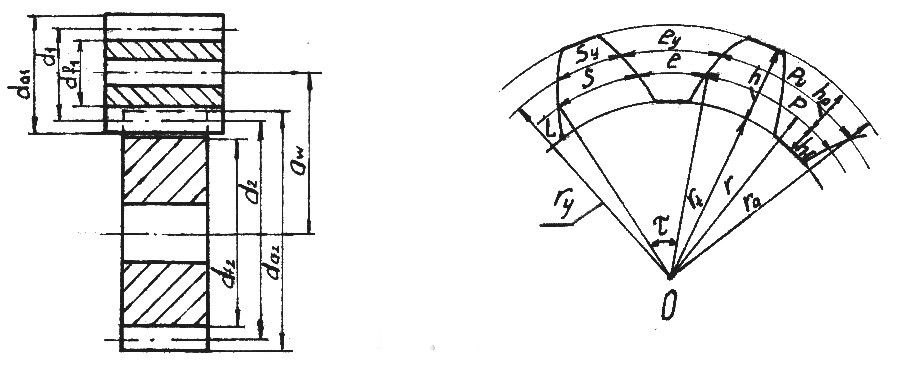
Окружной
шаг зубьев:
![]()
где Py – окружной шаг;
Sy – окружная толщина зуба;
ey – окружная ширина впадины.
Модуль и шаг зависят от окружности, к которой они относятся.
Расчетный
модуль зубчатого колеса:
![]()
где P – шаг по делительной окружности (делительный шаг).
Диаметр делительной окружности
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Особенности геометрии косозубых, шевронных и конических передач
У
косозубых колес различают окружной
шаг Pt
(в
торцовом сечении), нормальный шаг Pn
(в
нормальном сечении) и соответственно
кружной (торцовый) модуль
![]() ,
нормальный модуль
,
нормальный модуль
![]() .
.
Очевидны следующие соотношения:
![]()
![]()
![]()
![]()
1.3. Особенности геометрии конических колес
О сновные
параметры зацепления конической
прямозубой передачи
сновные
параметры зацепления конической
прямозубой передачи
![]()
где
![]() –
средний делительный диаметр; de
- внешний
делительный диаметр; Z–
число
зубьев ш.и.к;
–
средний делительный диаметр; de
- внешний
делительный диаметр; Z–
число
зубьев ш.и.к;
![]() –
средний
окружной модуль;
–
средний
окружной модуль;
![]() –
внешний
окружной модуль.
–
внешний
окружной модуль.
![]()
где
![]() –
коэффициент
ширины зубчатого венца;
–
коэффициент
ширины зубчатого венца;
![]() –
ширина
зубчатого венца;
–
ширина
зубчатого венца;
![]() –
внешнее
конусное расстояние.
–
внешнее
конусное расстояние.
Внешнее конусное расстояние
![]()
Высота
головки зуба
![]() и ножки
и ножки
![]() .
.
Диаметры вершин зубьев и впадин конического зубчатого колеса:
![]()
Передаточное
число при
![]() =
90°
=
90°
![]()
Среднее
конусное расстояние
![]()
Усилия в зацеплении зубчатых передач
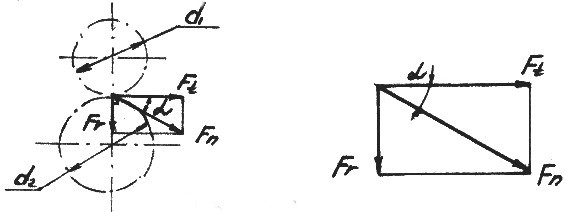
Прямозубая цилиндрическая передача
Силу Fn раскладывают на окружную Ft и радиальную Fr составляющие:
![]()
![]() –
изгибающая зуб,
–
изгибающая зуб,
![]() –
сжимающая
зуб,
–
сжимающая
зуб,
![]()
![]() –
угол главного
профиля,
–
угол главного
профиля,
где
![]() –
угол
зацепления; Т
– вращающий
момент на колесе (шестерне).
–
угол
зацепления; Т
– вращающий
момент на колесе (шестерне).
Косозубая и шевронная цилиндрические передачи.
![]()
![]()
где
![]() –
угол
зацепления косозубой передачи в
нормальном
сечении; β
– угол
наклона линии зуба.
–
угол
зацепления косозубой передачи в
нормальном
сечении; β
– угол
наклона линии зуба.
Конические зубчатые передачи. В зацеплении прямозубой конической передачи (см. рис. 1.7 б) нормальная сила Fn также
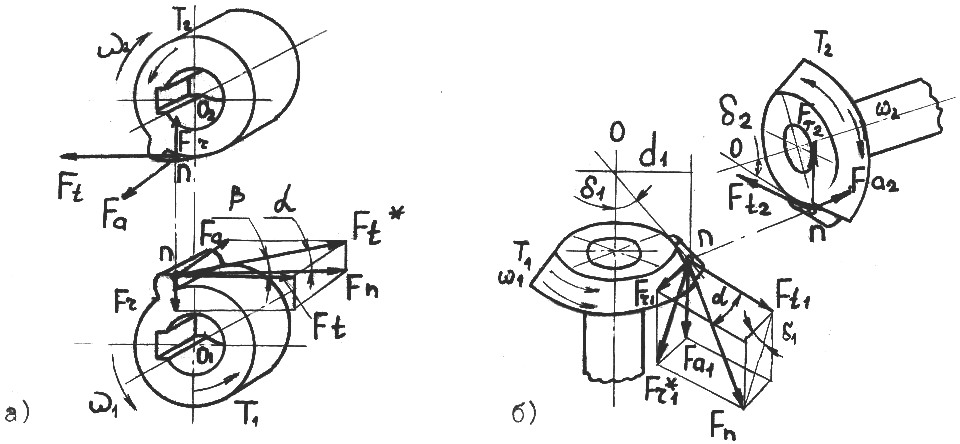
раскладывается на три составляющие, рассчитываемые по среднему делительному диаметру d:

1. Расчет зубьев на прочность при изгибе
Условие прочностной надежности зуба:
![]()
где
![]() –
максимальное
напряжение в опасном сечении зуба;
–
максимальное
напряжение в опасном сечении зуба;
![]() – допускаемое напряжение изгиба для
материала зуба.
– допускаемое напряжение изгиба для
материала зуба.
а). Прямозубые цилиндрические передачи
![]()
где Ft – окружная сила; BW – ширина венца колеса; m – модуль зацепления; yF– коэффициент формы зуба; KFα – коэффициент, учитывающий одновременное участие в передаче нагрузки нескольких пар зубьев (KFα = 1); KFβ – коэффициент концентрации нагрузки; KFυ – коэффициент динамической нагрузки.
б). Косозубые цилиндрические передачи
![]()
где
![]() –
коэффициент, учитывающий наклон
зубьев;
–
коэффициент, учитывающий наклон
зубьев;![]() –коэффициент
перекрытия;
–коэффициент
перекрытия;
![]() где
где
![]() –
коэффициент ширины колеса;
–
коэффициент ширины колеса;
![]() для
колес низкой твердости (не более 350 НВ)
;
для
колес низкой твердости (не более 350 НВ)
;
![]() (более 350 НВ).
(более 350 НВ).
Ширину зубчатых колес принимают в зависимости от диаметра шестерни.
в). Конические передачи
В опасном сечении зуба конического колеса максимальные напряжения
![]()
где
![]() –
экспериментальный коэффициент,
учитывающий пониженную нагрузочную
способность конических передач по
сравнению с цилиндрическими передачами
из-за конструктивных особенностей; m–
модуль
в среднем нормальном сечении зуба.
–
экспериментальный коэффициент,
учитывающий пониженную нагрузочную
способность конических передач по
сравнению с цилиндрическими передачами
из-за конструктивных особенностей; m–
модуль
в среднем нормальном сечении зуба.
= 0,85 – для конических прямозубых передач;
![]() 1-1.2
– для передач с круговыми зубьями.
1-1.2
– для передач с круговыми зубьями.
2. Расчет на контактную прочность активных поверхностей зубьев
Расчет зубьев выполняют для фазы зацепления в полюсе.
![]()
где
![]() –
максимальное
контактное напряжение на активной
поверхности зубьев;
–
максимальное
контактное напряжение на активной
поверхности зубьев;
![]() –
допускаемое
контактное напряжение.
–
допускаемое
контактное напряжение.
Контактные напряжения одинаковы для обоих колес, поэтому расчет выполняют для того колеса, у которого меньше.
Для расчета зубчатой передачи на контактную прочность необходимо иметь уравнение, связывающее максимальное напряжение с внешней нагрузкой и параметрами передачи.
а). Прямозубые и косозубые передачи
![]()
где
ZH
–
коэффициент,
учитывающий форму сопряженных
поверхностей; ZM–
коэффициент,
учитывающий механические свойства
материалов колес (модули упругости
Е1
и Е2
и коэффициенты Пуассона,
![]() и
и
![]() ).
ZM
=
275 – для стальных колес; Zε
– коэффициент,
учитывающий суммарную .длину
контактных линий.
).
ZM
=
275 – для стальных колес; Zε
– коэффициент,
учитывающий суммарную .длину
контактных линий.
![]() – для
прямозубых передач.
– для
прямозубых передач.
![]() – для косозубых
передач.
– для косозубых
передач.
![]() в предварительных
расчетах,
в предварительных
расчетах,
![]() –
из
таблиц.
–
из
таблиц.
![]() –
межосевое
расстояние;
–
межосевое
расстояние;
![]() –
ширина
колеса; U
– передаточное
число.
–
ширина
колеса; U
– передаточное
число.
принимают в зависимости от межосевого расстояния.
![]()
где
![]() – коэффициент ширины колеса.
– коэффициент ширины колеса.
б). Конические передачи (прямозубые)
Расчет
производить по формуле (1.23), где вместо
коэффициента
подставить
коэффициент
![]() (установлен экспериментально, учитывает
особенности прочности конических
передач ).
(установлен экспериментально, учитывает
особенности прочности конических
передач ).![]() 0,85
–для прямозубых.
0,85
–для прямозубых.
