
- •1 Основные кинематические величины
- •2 Движение по окружности
- •3 Криволинейное движение
- •4 Законы Ньютона
- •8 Центр масс
- •9 Степени свободы (механика)
- •10 Момент силы
- •11 Динамика твердого тела
- •12 Момент инерции
- •13 Теорема Штейнера
- •15 Работа и потенциальная энергия
- •2. Различают два вида механической энергии — потенциальная и кинетическая.
- •3. Выясним, чему равна потенциальная энергия тела, поднятого над Землей. Для этого найдем связь между работой силы тяжести и изменением потенциальной энергии тела.
- •4. При определении потенциальной энергии тела необходимо указывать уровень, относительно которого она отсчитывается, называемый нулевым уровнем.
- •5. Потенциальной энергией обладает любое деформированное тело. При сжатии или растяжении тела оно деформируется, изменяются силы взаимодействия между его частицами и возникает сила упругости.
- •Ламинарный и турбулентный режим течения жидкости
- •4.2.4.Адиабатный процесс
- •4.2.5. Политропный процесс
- •55 Первое начало термодинамики
- •§ 31. Распределение зарядов в проводнике. Клетка Фарадея.
- •Вопрос 98 «Закон Джоуля-Ленца для участка цепи»
- •99 «Правила Кирхгофа»
- •100 «Законы Фарадея для электролиза»
- •101 «Закон Ома для плотности тока в электролитах»
- •102 «Несамостоятельный газовый разряд»
- •103 «Самостоятельный газовый разряд»
- •104 «Плазма и ее свойства»
- •105 «Магнитная индукция»
- •117 «Диамагнетики и парамагнетики»
- •118 «Закон полного тока для магнитного поля в веществе»
- •119 «Основной закон электромагнитной индукции»
- •120 «Вращение рамки в магнитном поле»
- •121 «Явление самоиндукции»
- •122 «Явление взаимной индукции»
- •123 «Энергия магнитного поля»
- •124 «Вихревое электростатическое поле»
- •125 «Ток смещения»
- •126 «Уравнения Максвелла для электромагнитного поля»
13 Теорема Штейнера
Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика "Якоба Штейнера и голландского математика, физика и астронома %BD"Христиана Гюйгенса): "момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

где
JC — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m — масса тела,
d — расстояние между указанными осями.
Вывод
Момент инерции, по определению:
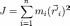
Радиус-вектор
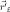 можно
расписать как разность двух векторов:
можно
расписать как разность двух векторов:
 ,
,
где
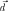 —
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:
—
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:
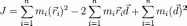
Вынося за сумму , получим:
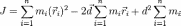
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Тогда:

Откуда и следует искомая формула:
,
где JC — известный момент инерции относительно оси, проходящей через центр масс тела.
14 Работа силы
Понятие “работа“ как физическая величина во всех энциклопедиях, справочниках и учебниках раскрывается как понятие “работа силы“ при описании прямолинейной механической формы движения. Правда, в физике применяется также и понятие “работа поля“, которое трактуется, как “работа сил поля“. В БСЭ работа силы определяется, как “мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения“. В метрологическом справочнике А.Чертова (1990) определение работы силы присутствует в виде словесной формулировки определяющего уравнения для элементарной работы силы F на элементарном перемещении dr без раскрытия ее физического содержания: dA = F dr . ( 1 ) На конечном перемещении A = Fr. Оба вышеприведенных определения относятся к механическим системам. На странице, посвященной обобщенному .1.07.html"уравнению состояния, приведены две формы записи главного определяющего уравнения: U dq = dW ( 2 ) и dW = U dq , ( 3 ) где dW − .1.07.html"энергетическое воздействие на систему, dq − приращение координаты состояния системы, U − .1.07.html"динамическое воздействие на систему. Там же было показано, что главное определяющее уравнение в форме (2) соответствует принципу причинности и должно применяться во всех случаях внешнего энергетического воздействия dW на систему. С определяющим уравнением (1) для работы силы dA совпадает лишь уравнение (3), если в качестве координаты состояния dq в механической прямолинейной форме движения принять перемещение dr, а в качестве динамического воздействия U принять силу F. Из чего следует, что работа силы dA, если ее определять по уравнению (1), не является энергетическим воздействием dW на механическую систему, несмотря на то, что работа силы имеет ту же размерность, ту же единицу и то же численное значение, что и энергия. Чтобы в механической прямолинейной форме движения соблюдался принцип причинности, уравнение (1) должно быть заменено уравнением F dr = dА . ( 4 ) При такой постановке вопроса понятие “работа“ можно применять не только в прямолинейной форме движения, и можно говорить не только о работе силы. С тем же успехом и с той же размерностью можно говорить и о .03.wra.html"работе вращающего момента M при вращательной форме движения, и о .03.hydr1.html"работе перепада давлений Δp при гидравлической объёмной форме движения, и о работе в других формах движения. В частности, уравнение (2) можно записать в виде: M dφ = dА ( 5 ) или Δp dV = dА , ( 6 ) где dφ − элементарный угол поворота; dV − элементарное перемещение объёма. На странице, посвященной .1.06.html"формам движения, показано, что выбор формы движения определяется выбором .1.05.html"координаты состояния. И уж по координате состояния определяется вид .1.07.html"динамического воздействия. В наших примерах выбор в качестве координаты состояния перемещения предопределяет то, что в качестве динамического воздействия появится сила, выбор угла поворота предопределяет появление вращающего момента, выбор объемного перемещения предопределяет появление перепада давлений. Именно такая причинно-следственная цепочка имеет место в физике, хотя при изучении физики по современной методике складывается впечатление, что всё наоборот. Лишь при рассмотрении понятия “работа сил поля“ причина и следствие меняются местами: силы взаимодействия зарядов поля становятся причиной, а работа этих сил − следствием. И поэтому данной ситуации соответствует главное определяющее уравнение в форме (3).
