29. Отыскание критических областей. Мощность критерия.

1) Отыскание правосторонних критических областей. Чтобы найти критическую область надо найти критическую точку. Для ее нахождения задают определенный уровень значимости , а затем при выполнении нулевой гипотезы вероятность выполнения неравенства P(K>k_кр)=. Далее критическая точка определяется по таблице приложений. Если после нахождения критической точки K>k_кр, то нулевую гипотезу отвергают, противном случае принимают.

2) отыскание левосторонних критических областей. Сводится к отысканию критической точки. Левосторонняя критическая область определяется неравенством: K<k_кр, где k_кр<0.

Критическую точку находят из требования, что при справедливости нулевой гипотезы, при заданном уровне значимости  выполняется равенство: P(K<k_кр)=.

3) отыскание двусторонних критических областей. Сводится к отысканию критических точек. Двусторонняя критическая область определяется неравенствами: K<k₁; K>k₂ , где k₂> k₁. Критическая точка определяется из требования, что пр справедливости нулевой гипотезы при заданном уровне значимости  выполняется равенство:P(K<k₁)+ P(K>k₂)=.

В частности, если при справедливости нулевой гипотезы можно получить распределения критерия K, симметричного относительно нуля, и как следствие задать критические точки, также симметричные относительно 0, т.е. получаем точки –k_кр и +k_кр, где k_кр>0.

Тогда P ( K < - k_кр ) = P ( K > + k_кр)=/2.

Мы строили критическую область, исходя из предположения, что вероятность попадания критерия в критическую область равна заданному уровню значимости  при справедливости нулевой гипотезы. Оказывается, целесообразно рассмотреть вероятность попадания критерия в критическую область справа при справедливости конкурирующей гипотезы Н₁. Т.е. гипотезу Н₀ отвергаем.

опр: Мощностью критерия называют попадание критерия в критическую область при справедливости конкурирующей гипотезы. Пусть для проверки гипотезы задан определенный уровень значимости  и фиксированный объем выборки n, тогда критическую область нужно строить так, чтобы мощность критерия была максимальна, при этом ошибка второго рода сводится к минимуму.

30. Сравнение двух дисперсий нормальных генеральных совокупностей.

На практике задача сравнения дисперсий возникает в том случае, если требуется сравнить точность приборов, инструментов либо методов измерений. Очевидно, точнее тот прибор, инструмент, метод, для которого дисперсия минимальна.

Пусть генеральные совокупности Х и У распределены нормально. По независимым выборкам с объемом соответственно n₁ и n₂, извлеченным из соответствующей генеральной совокупности вычислены исправленные выборочные дисперсии S_x² и S_y². Требуется по исправленным дисперсиям при заданном уровне значимости  проверить нулевую гипотезу о равенстве дисперсий генеральной совокупности Н₀:D(X)=(Y).

Если окажется, что гипотеза Н₀ верна, т.е. генеральные дисперсии равны, то различие выборочных дисперсий незначимо, что объясняется случайными причинами. Например, случайным отбором элементов выборки. Например, если различие исправленных выборочных дисперсий незначимо, а они вычислены по выборке, показывающей точность измерения, то это означает, что оба прибора, на которых производятся измерения, имеют одинаковые точности. Если гипотеза Н₀ отвергнута, т.е. исправленные выборочные дисперсии различаются значимо, то это не может объясняться случайными причинами, а означает, что сами генеральные дисперсии различны.

В качестве критерия проверки гипотезы Н₀ вводят случайную величину F: 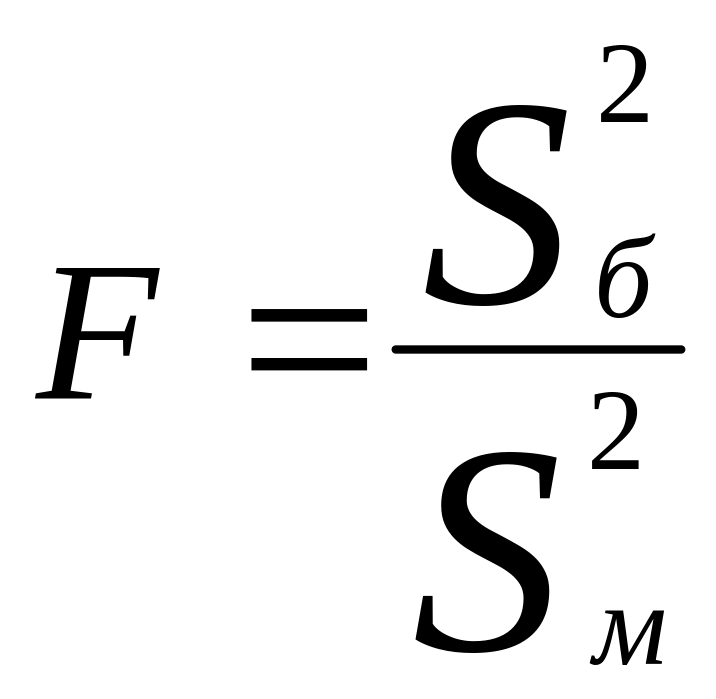. Величина f при справедливости гипотезы Н₀ имеет распределение Фишера – Снедекорда с k₁=n₁-1 и k₂=n₂-1 степенями свободы, где k₁ – степень свободы выборки с наибольшей дисперсией. Ее значение (случайной величины F) по заданному уровню значимости , а также степенями свободы k₁ и k₂ определяют по таблице критических точек распределения Фишера – Снедекорда. (F(,k₁,k₂)) и по полученной критической точке определяют критическую область. Критические области в зависимости от конкурирующей гипотезы различаются:

Случай 1:

Гипотеза Н₀: D(X)=D(Y)

Гипотеза Н₁: D(X)>D(Y)

В этом случае строят одностороннюю критическую область, а именно правостороннюю, исходя из требования, чтобы вероятность попадания критерия в критическую область, при справедливости Н₀ была равна заданному уровню значимости .

P(F<F_кр(, k₁, k₂))=. Критическую точку F_кр(, k₁, k₂) находят по таблице приложений, учитывая, что k₁ - степень свободы выборки с наибольшей исправленной дисперсией. Далее вычисляют наблюдаемое значение критерия: 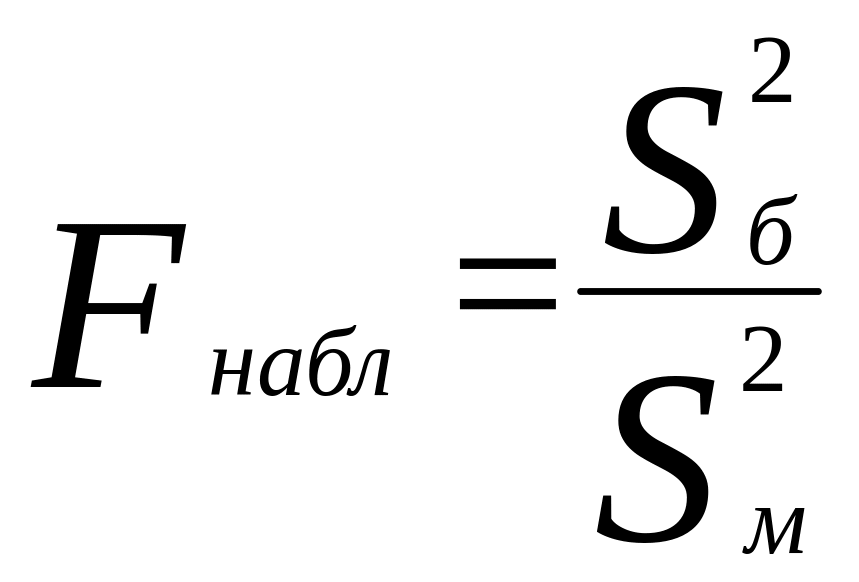, и сравнивают между собой F_кр и F_набл.

Если F_набл<F_кр, то Н₀ – отвергают, если F_набл>F_кр, то Н₀ – принимают.

В этом случае строят двухстороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область при справедливости нулевой гипотезы была равна заданному уровню значимости .

Нам нужно выбрать границы двусторонней критической области. Оказывается, что наибольшая мощность критерия в любом из двух интервалов критической области равна /2. Т.о., если обозначить через F₁ левую границу критической области, а через F₂ – вторую, тогда P(F<F₁)=P(F>F₂)=/2. Мы видим, что достаточно найти критические точки, чтобы найти саму критическую область. Правую критическую область F₂=F_кр(/2, k₁, k₂) находим по таблице приложений. При этом не только вероятность попадания критерия в правую часть критической области равна /2, но и вероятность попадания в левую часть критической области также равна /2. Т.к. эти события несовместны, то P(F<F₁;F>F₂)=/2+/2=. Далее находят F_набл: и сравнивают F_набл с F_кр.

Если F_набл<F_кр, то Н₀ – отвергают, если F_набл>F_кр, то Н₀ – отвергают.