Опуклі множини

О1. Відкритим, замкненим відрізком з кінцями в елементах x,y лінійного простору називаються відповідно множини елементів цього простору .

О2. Відкритою, замкненою кулею в лінійному нормованому просторі з центром в точці x₀ і радіусом r називається множина всіх елементів цього простору, віддаль від яких до елемента x₀ відповідно , і позначають ,

.

Сферою в лінійному нормованому просторі з центром в точці x₀ радіуса r називається множина всіх елементів цього простору, віддаль яких до елемента x₀ дорівнює r

.

О3. Множину лінійного простору називають опуклою, якщо вона містить довільний замкнутий відрізок, кінці якого належать цій множині, тобто:

Приклад.

1. .

Використовуючи означення опуклої множини, означення замкнутого відрізка і критерій підпростору , маємо:

2. Будь-який відрізок лінійного простору – опукла множина в цьому просторі

а)

б)

3. Зсув довільної опуклої множини на довільний елемент x₀ є опукла множина

.

Використовуючи означення множини , означення відрізка і означення опуклої множини, маємо:

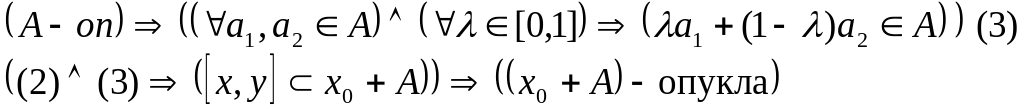
4.Довести, що довільна куля є опуклою множиною, тобто: - опукла.

Теорема Перетин довільної кількості опуклих множин є опукла множина.

О4. Замкненою, відкритою опуклою оболонкою n-елементів лінійного простору називають множину всіх відповідно лінійних комбінацій цих елементів з невід’ємними додатніми коефіцієнтами, сума коефіцієнтів яких дорівнює 1 і позначають

, .

Приклад:

1. n=2, то використовуючи означення 4 і означення відрізка, одержимо

Критерії опуклості множини:

З означення опуклості множини в ЛНП випливає, що опуклими множинами на прямій є проміжки

Критерії опуклості множини

Непорожня множина лінійного простору опукла тоді і тільки тоді, коли довільна замкнута лінійна оболонка n-елементів цієї множини міститься в цій множині. Порожню множину також вважають опуклою.

Доведення:

Якщо , то використовуючи означення замкнутого відрізка і означення опуклої множини, одержимо:

Необхідність доведемо методом математичної індукції.

1. Припустимо, що твердження істинне при n=2, тобто

.

2. Припустимо, що твердження істинне при , тобто

.

3. Використовуючи припущення 2 і 1, доведемо, що твердження вірне при .

.

Використовуючи означення включення, достатньо довести

.

З означення опуклої оболонки випливає, що

.

Не обмежуючи загальності будемо вважати, що , тобто Тоді

З (4) за означенням опуклої оболонки випливає

З (4) згідно з твердженням 1 випливає, що: . Отже, за принципом математичної індукції твердження істине при довільному . Критерій доведено.

Наслідок (про мінімальність опуклої оболонки).

Опукла оболонка будь-яких n-елементів, містяться в усіх опуклих множинах, які містять ці елементи.

Використовуючи необхідність в критерії опуклості множини, означення операції перетину, одержимо:

Опуклі функціонали

О1. Функціонал називається строго опуклим донизу (догори) на опуклій множині, якщо значення цього функціонала в довільній точці відкритого відрізка, кінці якого належать множині, строго менше (більше) ніж значення відповідної ординати відрізка, що проходить через точки і в нерівності має знак рівності тоді і тільки тоді коли кінець і початок відрізка співпадають

О2 Функціонал називається не строго опуклим на опуклій множині, якщо значення цього функціонала в довільній точці замкнутого відрізка, кінці якого належать множині, менше рівне ніж значення довільної ординати відрізка, що проходить через точки

Приклад 1.

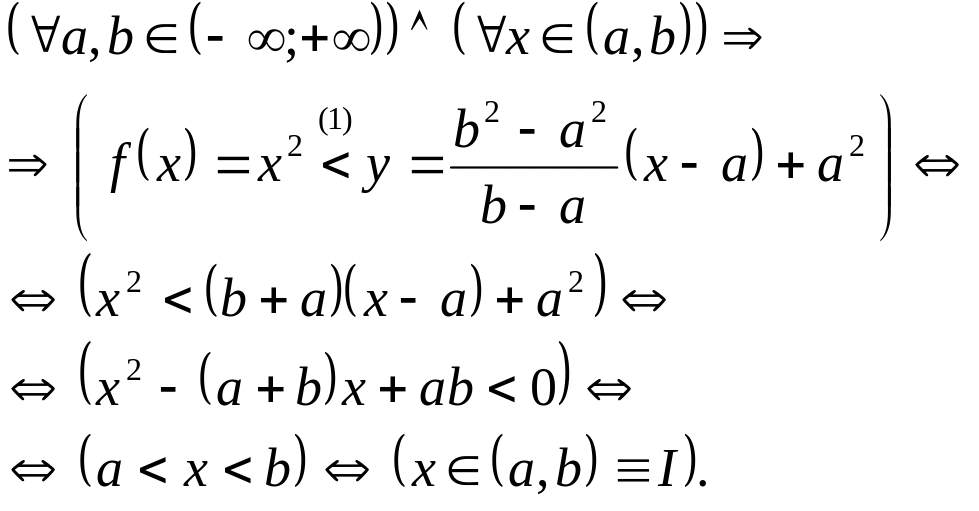
Приклад 2.

Теорема 1 (критерії Ієнсена строгої опуклості функціонала).

Функціонал строго опуклий донизу на опуклій множині, тоді і тільки тоді коли значення цього функціонала в довільній точці довільної відкритої опуклої оболонки довільних n-елементів цієї множини, , строго менше ніж відповідна опукла оболонка образів цих елементів і в нерівності має місце знак рівності тоді і тільки тоді коли всі елементи рівні між собою, тобто:

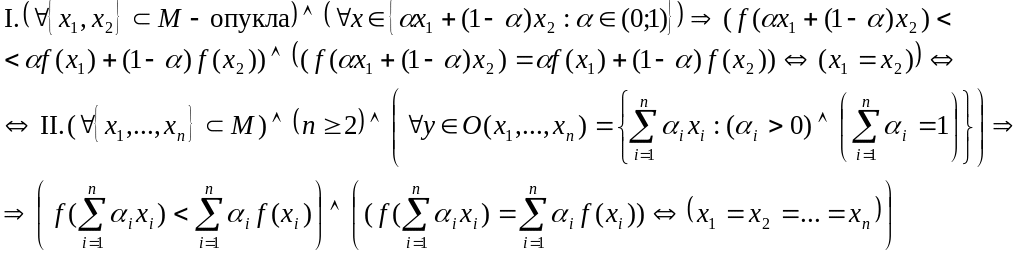
Достатність

Якщо , то використовуючи (II) матимемо:

Необхідність доведемо методом математичної індукції.

1. Перевіримо, чи твердження істинне при n=2.

2. Припустимо, що твердження вірне при .

3. Доведемо, використовуючи 2 і 1, що твердження вірне при .

Використовуючи критерій опуклості множини, твердження (2) і (1), одержимо:

Отже, за принципом математичної індукції твердження істине при довільному натуральному .

О1. Звуженням значень функціонала f на довільний відрізок з кінцями в точках x і y називають функцію

Теорема 2 (критерії опуклості функціонала)

Функціонал строго опуклий на опуклій множині тоді і тільки тоді, коли звуження цього функціонала на довільний відрізок з кінцями, що належать цій множині є функцією відповідно строго опуклою донизу (догори) не строго опуклою донизу (догори) на сегменті [0;1], тобто

Необхідність (І ІІ).

Використовуючи (1) і О.1, одержимо:

Достатність (ІІ І).

Використовуючи (ІІ), (1) і О.1, одержимо: