
- •Властивості віддалі. Означення метричного простору і найкращого наближення елемента множини метричного простору.
- •Приклади метричного простору, елементами яких є довільні об’єкти.
- •Лінійні простори. Приклади
- •Лінійні нормовані простори. Приклади. Властивості норми.
- •3. Неперервність норми.
- •4. Властивість рівномірної неперервності функціонала норми.
- •Евклідові простори.
- •Означення і приклади евклідових просторів.
- •Опуклі множини
- •Критерії опуклості множини:
- •Опуклі функціонали
- •Достатні умови опуклості функції від однієї змінної.
- •Теорема 1 (достатня умова строгої опуклості функції від однієї змінної в точці).
- •Критерії знаковизначеності матриць
- •Теорема 1 (критерії Сильвестра знаковизначеності і невизначеності матриць)
- •Достатні умови опуклості функції від багатьох змінних
- •Теорема 1 (достатня умова строгої опуклості функції від n-змінних)
- •1. Методом перерізів встановимо вид поверхні Якщо:
- •Нескінченна диференційовність добутку функцій і складної функції
- •Нерівність між середніми
4. Властивість рівномірної неперервності функціонала норми.
Функціонал норми рівномірний неперервний на всьому лінійному нормованому просторі, тобто:
![]()
Доведення:
Використовуючи нерівність 2 і означення рівномірного неперервного функціонала, одержимо:
![]()
О6.
Функціонал називається
неперервним в точці x0
лінійного нормованого
простору, якщо
знайдеться
таке, що для
![]() елемента
х з
простору, віддаль якого до х0
менша
випливає,
що віддаль між образами елементів х
і х0
менша
,
тобто:
елемента
х з
простору, віддаль якого до х0
менша
випливає,
що віддаль між образами елементів х
і х0
менша
,
тобто:
![]() .
.
Кожен рівномірно неперервний функціонал є неперервним.
Наслідок.
Функціонал норми неперервний
на всьому лінійному нормованому просторі,
тобто:
![]() .
.
Доведення:
Якщо
![]() і
і
![]() ,
то з означення 5 випливає означення 6 і
наслідок доведено.
,
то з означення 5 випливає означення 6 і
наслідок доведено.
Евклідові простори.
Означення і приклади евклідових просторів.
О1. Евклідовим простором називається лінійний простір над полем С або R, для елементів якого введено поняття скалярного множення.
Скалярним множенням в лінійному
просторі називається відображення
![]() ,
яке кожну впорядковану пару елементів
відображає в єдине дійсне або комплексне
число, яке називається скалярним добутком
цих елементів і позначається
,
яке кожну впорядковану пару елементів
відображає в єдине дійсне або комплексне
число, яке називається скалярним добутком
цих елементів і позначається
![]() при
цьому виконуються такі аксіоми:
при
цьому виконуються такі аксіоми:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Приклад.
1.

2.
![]()
Перевіримо виконання аксіоми 1 скалярного добутку.
![]() використовуючи
означення евклідового простору і
означення скалярного добутку, і
властивості комплексних спряжених
чисел, одержимо:
використовуючи
означення евклідового простору і
означення скалярного добутку, і
властивості комплексних спряжених
чисел, одержимо:
![]()
Перевіримо виконання аксіоми 3 скалярного добутку. Використовуючи означення нульової послідовності, маємо:

3.

1)![]()
2)
![]()
Використовуючи означення
скалярного множення, означення рівності
елементів в просторі
![]() і властивості інтеграла Лебега зв’язані
з нерівностями
і властивості інтеграла Лебега зв’язані
з нерівностями
3)
 .
.
Властивості скалярного добутку:
Означення норми в евклідовому просторі. Нерівність Шварца
Властивості:
1.
![]()
2. Скалярний добуток довільного елемента на нульовий елемент дорівнює 0, тобто:
![]()
3. Нерівність Шварца:
Модуль скалярного добутку будь-яких двох елементів евклідового простору не перевищує добутку норм цих елементів і в нерівності має місце знак рівності т і т.д. коли ці елементи лінійно залежні, тобто:
![]()
Використовуючи аксіоми скалярного добутку і властивість 1 маємо:
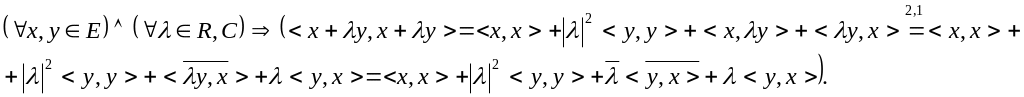 (1)
(1)
а)
![]() .
.
б)
![]() .
.
Покладемо
![]() і підставимо в (1). Тоді
і підставимо в (1). Тоді
![]()
![]() В
нерівності Шварта має місце знак рівності
тоді і тільки тоді, коли має місце знак
рівності в нерівності (2).
В
нерівності Шварта має місце знак рівності
тоді і тільки тоді, коли має місце знак
рівності в нерівності (2).
![]()
Нерівність доведена.
О2. Нормою довільного елемента евклідового простору називається корінь квадратний з скалярного добутку цього елемента на себе, тобто:
![]()
О3. Променем в лінійному просторі породжений ненульовим елементом x називають множину всіх елементів цього простору, пропорційних елементу x з невід’ємним коефіцієнтом пропорційності і позначають
![]()
4. Норма суми двох довільних елементів евклідового простору не перевищує сумі норм цих елементів і в нерівності має місце знак рівності тоді і тільки тоді коли елементи належать одному й тому ж променю, тобто:
![]()
Доведення:
Використовуючи означення
норми, аксіоми скалярного добутку і
властивості
![]() спряжених комплексних чисел і нерівність
Шварца, одержимо:
спряжених комплексних чисел і нерівність
Шварца, одержимо:
![]()
В нерівності (1) має місце знак рівності, коли має місце знак рівності в нерівності Шварца і реальна частина комплексного числа дорівнює модулю цього комплексного числа, тобто
![]() З
означення скалярного добутку і останньої
нерівності випливає, що для
З
означення скалярного добутку і останньої
нерівності випливає, що для
![]() виконуються аксіоми норми. Тому евклідів
простір є нормованим.
виконуються аксіоми норми. Тому евклідів
простір є нормованим.
