Елементи
функціонального аналізу і теорії
наближення
функцій.
Метричні простори.
Властивості віддалі. Означення метричного простору і найкращого наближення елемента множини метричного простору.
З шкільного курсу математики
відомо, що віддаль між двома точками
на прямій визначається так:
;
на площині:
і
в тривимірному просторі:
.
З означення границі послідовності
випливає, що в цьому означенні
фігурує поняття віддалі. Оскільки
означення границі використовується
при формулюванні багатьох понять
математики, то поняття віддалі відіграє
важливу роль в усіх розділах математики.
О1. Нехай
.
Віддаллю між
елементами множини
називається відображення
,
тобто дійсну функцію
від двох дійсних змінних, яка задовільняє
аксіоми Лінденбаума: І.
;
ІІ.
.
Властивості віддалі.
Теорема про невід’ємність і симетричність віддалі.
Віддаль між будь-якими двома елементами невід’ємна і симетрична, тобто:
а)
;
б)
.
Доведемо твердження б.
Покладемо
.
Тоді, використовуючи аксіоми Лінденбаума,
маємо:
(1).
Якщо
замінити на
то аксіому І можна записати так:
(2).
Покладемо
.
Тоді з нерівності (2), використовуючи
аксіоми Лінденбаума, одержимо:
(3).
З (3) і (1) випливає, що
.
Доведемо твердження а.
Покладемо
.
Тоді, використовуючи аксіоми Лінденбаума,
маємо:
.
Теорему доведено.
О2. Метричним простором
називають непорожню
множину, для елементів якої введено
поняття віддаль і позначають
.
Термін метричний простір ввів французький математик Фреше 1919 р., а «три» аксіоми простору — німецький математик Хаусдорф.
З аксіоми I
Лінденбаума і симетричності віддалі
випливає нерівність трикутника
.
Доведемо узагальнену нерівність
трикутника.
.
Доведення проведемо методом математичної індукції.
1. Перевіримо істиність
нерівності при
,
тобто
.
.
Остання нерівність є нерівністю
трикутника.
2. Припустимо, що нерівність
істина при
,
тобто
.
3. Доведемо, використовуючи
припущення і нерівність трикутника, що
нерівність істина при
,
тобто
Використовуючи нерівність
трикутника і припущення, маємо:
.
Позначимо через
Доведемо, що
простір.
Перевіримо виконання аксіоми II.
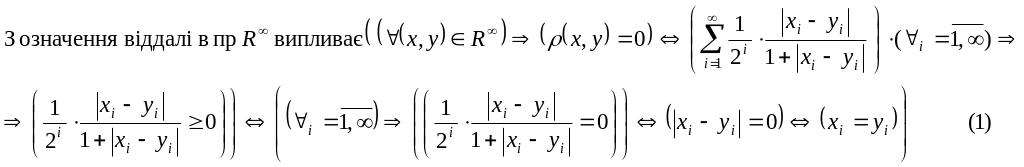
З (1) за означенням рівності
послідовностей випливає, що
.
Отже виконується аксіома ІІ Лінденбаума.
Перевіримо виконання аксіоми І. Доведемо нерівність
(І)
I спосіб. Нехай
, де
.
Тоді
Тому, згідно з достатньою
умовою монотонності функції, функція
строго зростаюча на проміжку
.
Використовуючи монотонність функції
і властивості модулів, одержимо:
Нерівність І доведена.
ІІ спосіб. Нерівність (І)
рівносильна нерівності
Використовуючи нерівність I одержимо:
Основні задачі теорії наближень зводяться
до знаходження віддалі від елемента x
до множини F
метричного простору, тобто до знаходження
величини
,
яку називають найкращим
наближенням елемента
x множиною
F і
позначають
і до знаходження віддалі між двома
множинами
,
яку називають найкращим наближенням
множини М
множиною F і
позначають
.
Приклади метричного простору, елементами яких є довільні об’єкти.
Нехай
Доведемо, що простір
,
який називають простором ізольованих
точок, метричний. Перевіримо виконання
аксіоми І Лінденбаума, тобто
Використовуючи означення віддалі в
просторі ізольованих точок, маємо:
а)
б)
.
в)
.
Інших випадків для елементів
множини
бути
не може. Отже аксіома І Лінденбаума
виконується.
Використовуючи означення віддалі в просторі ізольованих точок, одержимо:
.
Отже виконується аксіома ІІ Лінденбаума,
і простір ізольованих точок метричний.
Нехай простір
- метричний і
.
Доведемо, що простір
- метричний.
Перевіримо виконання аксіоми I Лінденбаума. Використовуючи нерівність I і аксіому Лінденбаума для простору , одержимо:
.
Отже виконується аксіома І Лінденбаума.
Використовуючи означення віддалі в
просторі
і аксіому ІІ Лінденбаума, маємо:
.
Отже виконується аксіома ІІ Лінденбаума,
і простір
- метричний.