
- •Глава 4. Интерференция.
- •4.1. Интерференция световых волн.
- •4.2 Когерентность.
- •4.3 Влияние немонохроматичности света на интерференционную картину.
- •4.4 Оценка протяженности источника.
- •4.5 Примеры получения интерференционной картины.
- •4.6 Интерференция света при отражении от тонких пленок.
- •4.7 Интерференция в тонком клине.
- •4.8 Кольца Ньютона.
- •Двухлучевые интерферометры.
- •4.10 Многолучевой интерферометр Фабри–Перо
- •4.11 Примеры решения задач
Глава 4. Интерференция.
4.1. Интерференция световых волн.
В обычных условиях в пространстве распространяется одновременно бесчисленное множество световых волн от различных источников излучения или волн, отраженных и рассеянных поверхностями предметов. Из опыта мы знаем, что такое взаимное наложение друг на друга всего бесконечного множества излучений не мешает их распространению в пространстве, так как видимые нами предметы совершенно не искажаются, несмотря на то, что свет, приносящий в глаз информацию о внешних предметах, на своем пути много раз пересекался с другими световыми лучами. Такой независимый характер каждого из световых процессов обусловлен тем, что воздействие на среду, в которой распространяется свет, со стороны электрических и магнитных полей, различных излучений не зависит от того, имеются ли в этой среде другие электромагнитные излучения или нет. Равным образом это означает, что электрические и магнитные поля различных электромагнитных волн при распространении в вакууме не изменяют взаимно свое направление, величину напряженности и другие характеристики. Это положение было названо принципом суперпозиции или принципом независимости электромагнитных волн.
При взаимодействии световых волн излучений особый интерес представляет сложение двух волн одинаковой частоты. В этом случае имеет место явление интерференции.
Пусть две монохроматические световые волны
![]() ,
,
![]()
с
одинаковой круговой частотой
![]() (следовательно, соответствующие длины
волн
(следовательно, соответствующие длины
волн
![]() и частоты
и частоты
![]() одинаковы) складываются в точке
одинаковы) складываются в точке
![]() .
.
![]() ,
,
![]() - начальные фазы колебаний.
- начальные фазы колебаний.

![]()
![]() ,
,
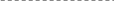 *
Р
*
Р
![]() ;
;

![]()
![]() .
.
Рис. 4.1
Квадрат амплитуды результирующего колебания не равняется сумме квадратов амплитуд складывающихся колебаний, т. е. энергия результирующего колебания не равна сумме энергий складывающихся колебаний. Результат сложения зависит от разности фаз исходных колебаний и может иметь любое значение в пределах от
![]() до
до
![]()
![]()
![]()
Практически мы никогда не имеем дела со строго гармоническими колебаниями, т. е. колебаниями, длящимися бесконечно долго с неизменной амплитудой. Обычно колебания время от времени обрываются и возникают вновь уже с иной, нерегулярно измененной фазой, т. е. не являются строго гармоническими. В таком случае и результирующая интенсивность ( ) также меняется с течением времени.
Наблюдая
эту интенсивность, мы могли бы получить
изменяющиеся значения; однако, для этого
необходимо применить для наблюдения
прибор, который реагировал бы достаточно
быстро, чтобы отмечать изменения
![]() .
В противном случае мы не сможем следить
за всеми изменениями
.
В этом плане человеческий глаз также
является несовершенным «прибором», т.
к. видимому свету (
.
В противном случае мы не сможем следить
за всеми изменениями
.
В этом плане человеческий глаз также
является несовершенным «прибором», т.
к. видимому свету (![]() )
соответствует
)
соответствует
![]() ,
а реакция глаза составляет только
,
а реакция глаза составляет только
![]() .
Таким образом мы будем рассматривать
только некоторое среднее
во времени значение
интенсивности
.
.
Таким образом мы будем рассматривать
только некоторое среднее
во времени значение
интенсивности
.
Под интерференцией понимают широкий круг явлений, в которых при наложении пучков света от двух и более когерентных источников результирующая интенсивность (освещенность экрана) не равна сумме интенсивностей отдельных пучков, а возникают чередования светлых и темных участков – интерференционная картина. Под когерентностью понимают источники, испускающие волны одной частоты и колеблющиеся с постоянной разностью фаз. Интерференцию излучений от двух независимых источников света визуально наблюдать нельзя. Необходимо излучение от одного источника разделить на два или более пучка для наблюдения
устойчивой интерференционной картины.
![]()
![]() - интерференция отсутствует.
- интерференция отсутствует.
![]()
![]()
![]()

![]() интерференционный
интерференционный
![]() член
член
И
![]() .
Поверхности равных интенсивностей
определяются уравнением
.
Поверхности равных интенсивностей
определяются уравнением
![]() и представляют собой плоскости,
перпендикулярные к вектору
и представляют собой плоскости,
перпендикулярные к вектору
![]() .
Расстояние
.
Расстояние
![]() между соседними плоскостями максимальной
(или минимальной) интенсивности
определяется условием :
между соседними плоскостями максимальной
(или минимальной) интенсивности
определяется условием :
![]() .
.
Если модули волновых
векторов
![]() и
и
![]() одинаковы
одинаковы
и
равны
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
.
Рис. 4.2
В
случае, когда волны распространяются
под малым углом друг к другу (![]() )
справедливо приближение:
)
справедливо приближение:
![]() ,
тогда
,
тогда
![]() .
Так как
.
Так как
![]() ,
следовательно
,
следовательно
![]() ,
где
,
где
![]() - угол, под которым видны когерентные
источники, создающие интерференционную
картину, из точки наблюдения.
- угол, под которым видны когерентные
источники, создающие интерференционную
картину, из точки наблюдения.
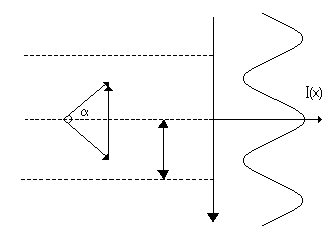
В первые
экспериментальная установка для
демонстрации интерференции света была
осуществлена Томасом Юнгом в
начале XIX в.
первые
экспериментальная установка для
демонстрации интерференции света была
осуществлена Томасом Юнгом в
начале XIX в.

S1
Q2
Р
Q1
S2
С
В
S
В
a
б
Рис. 4.3. Схема опыта Юнга.
CSB = 2 – апертура интерференции для любой точки поля.
S1 C Q1 = S2 C Q2 = 2 – апертура перекрывающихся пучков для бесконечно удаленного экрана.
C Р В = – угол, под которым видны когерентные источники, создающие интерференционную картину, из точки наблюдения Р.
Источником
света служит ярко освещенная щель
![]() ,
от которой световая волна падает на две
узкие щели С и В, освещаемые таким образом
различными участками одного и того же
волнового фронта. Световые пучки,
проходящие через малые отверстия С и
В, расширяются и частично перекрываются,
создавая интерференцию. При расположении
Юнга апертура
интерференции
(угол между выходящими из источника
интерферирующими лучами) 2
= CSB
определяется
отношением расстояния между щелями С
и В к расстоянию от
до СВ.
,
от которой световая волна падает на две
узкие щели С и В, освещаемые таким образом
различными участками одного и того же
волнового фронта. Световые пучки,
проходящие через малые отверстия С и
В, расширяются и частично перекрываются,
создавая интерференцию. При расположении
Юнга апертура
интерференции
(угол между выходящими из источника
интерферирующими лучами) 2
= CSB
определяется
отношением расстояния между щелями С
и В к расстоянию от
до СВ.
Наблюдаемая
интерференционная картина будет
определяться модулем разности оптических
путей
![]() (рис. 4.4).
(рис. 4.4).
m λ,
то max .
λ,
то max .
Если
Δx/2![]()
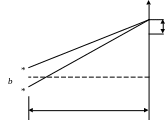
mλ + λ/2 , то min.

l1
l2
L
m
Если
 .
.
mλ + λ/2 в () Р
Рис. 4.4.
![]()
![]()
![]()

Если
![]() ,
то
,
то
![]() ,
тогда
,
тогда
![]()
![]()
Так
как
![]() ,
а
,
а
![]() и
и
![]() ,
то
,
то
![]()
![]()
![]() .
.
![]()
