Задача № 8.

Определить доверительный интервал для оценки с надежностью неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если известно выборочное среднее , объем выборки n и генеральное среднее квадратическое отклонение . (См. исходные данные в таблице).

Примеры решения задач к контрольной работе №3

Пример 1. Исследовать сходимость числового ряда

.

Решение. Имеем u_n = , u_n+1 = . Применяя признак Даламбера, вычислим

l = = = = = 0 < 1.

По признаку Даламбера данный ряд сходится.

Пример 2. Исследовать сходимость числового ряда

.

Решение. Введем функцию f (x) = , удовлетворяющую условиям и исследуем сходимость, используя интегральный признак. Для этого вычислим

= = =

= = - = .

Несобственный интеграл сходится, следовательно, сходится и данный ряд

Пример 3. Найти интервал сходимости степенного ряда

.

Решение. Составим ряд из модулей членов данного ряда и вычислим l = =

= = .

По признаку Даламбера ряд сходится при l < 1, отсюда

< 1 или |x| < 3. Следовательно, ряд абсолютно сходится при x (-3,3). Исследуем сходимость ряда в граничных точках. При x =3 и x = -3 из данного ряда получаем соответственно числовые ряды и ^. Из интегрального признака сходимости следует, что эти ряды сходятся абсолютно, поэтому интервалом сходимости данного ряда является промежуток [-3,3].

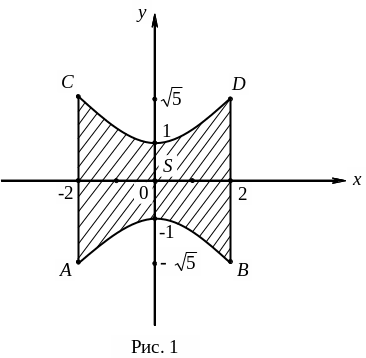
Пример 4. Определить пределы интегрирования интеграла , если область интегрирования S (рис. 1) ограничена гиперболой и двумя прямыми и (имеется в виду область, содержащая начало координат).

Решение. Область интегрирования ABCD (рис. 1) ограничена прямыми и и двумя ветвями параболы: и .

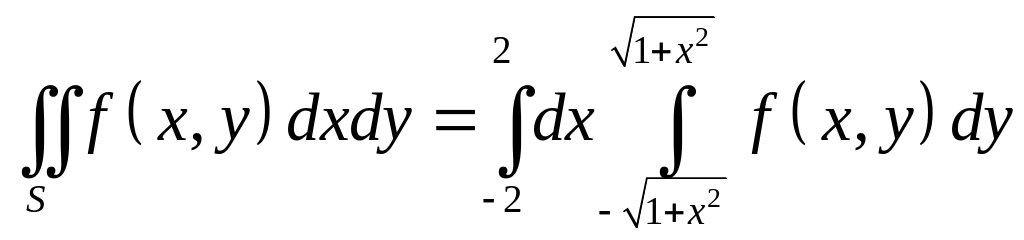
Пример 5. Вычислить двойной интеграл , где D – прямоугольник:

Решение.

Пример 6. Вычислить двойной интеграл: где D – треугольник

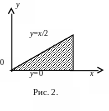
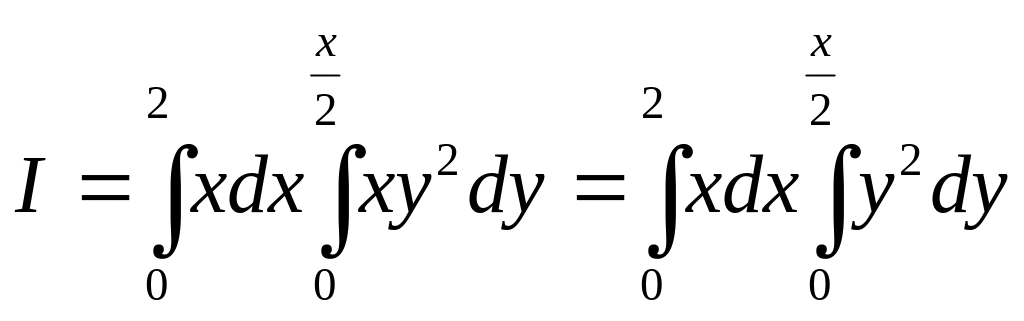
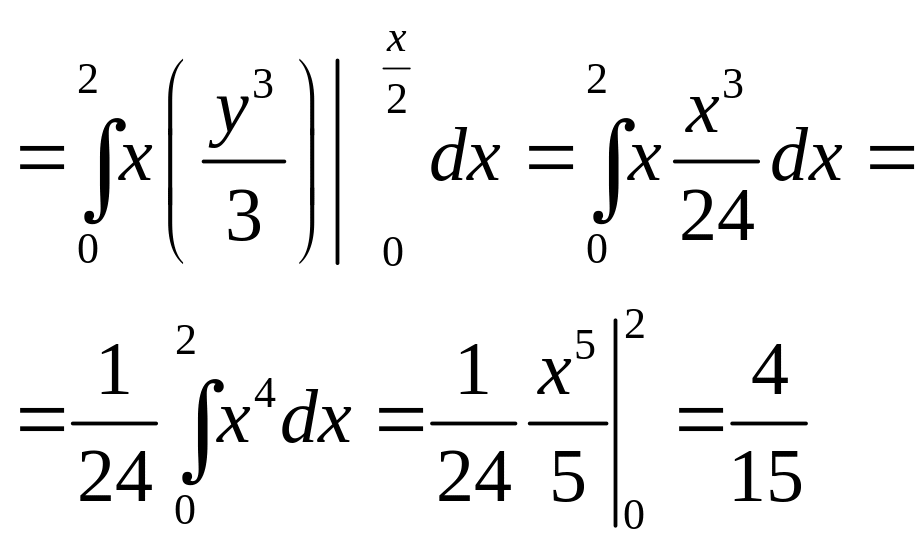
Пример 7. Поменять порядок интегрирования:

, где D: x=1, x=2, y=x; y=2x.

Решение.

Рис. 3.

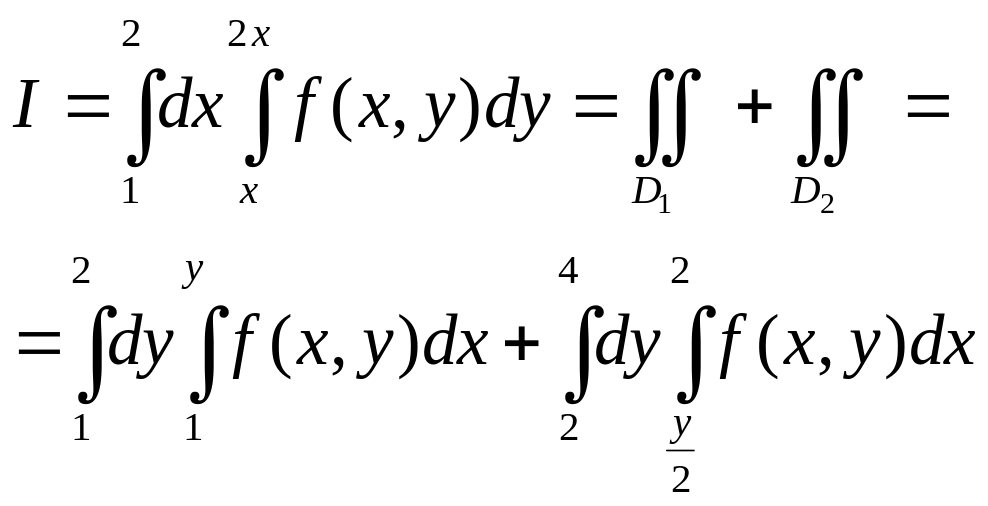
Пример 8. Изменить порядок интегрирования в двойном интеграле:

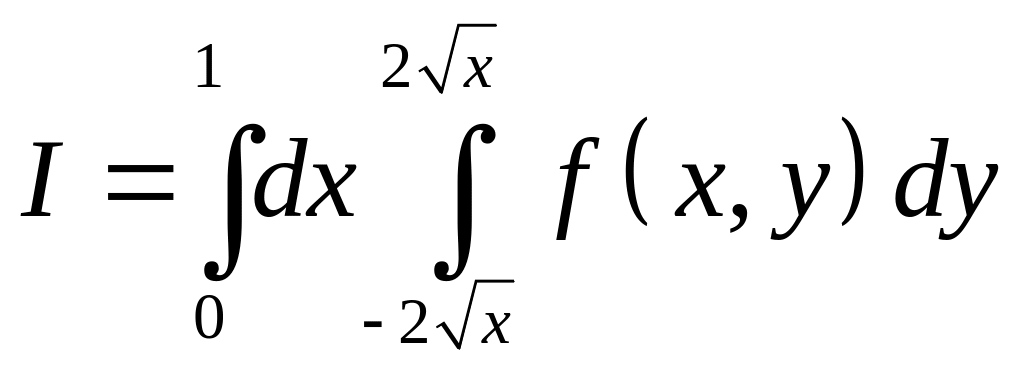
Решение. Зная пределы интегрирования, найдем границы области интегрирования D: , , , и построим их (рис. 4). Область D располагается в полосе и ограничена сверху и снизу соответствующими ветвями параболы

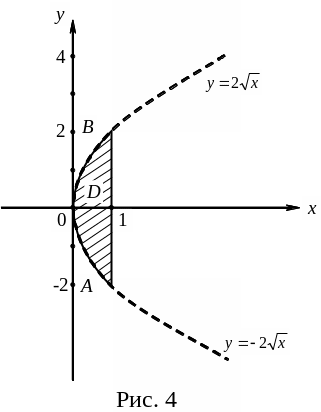
Найдем новые пределы внешнего (по у) и внутреннего (по х) интегрирования. Так как область D проецируется на ось Оу в отрезок АВ, то пределами внешнего интегрирования являются ординаты точек А и В, т. е. и соответственно. Левой границей области является кривая (уравнение параболы разрешено относительно х), а правой – прямая . Таким образом, двойной интеграл I с измененным порядком интегрирования запишется в виде

.

Пример 9. Вычислить интеграл

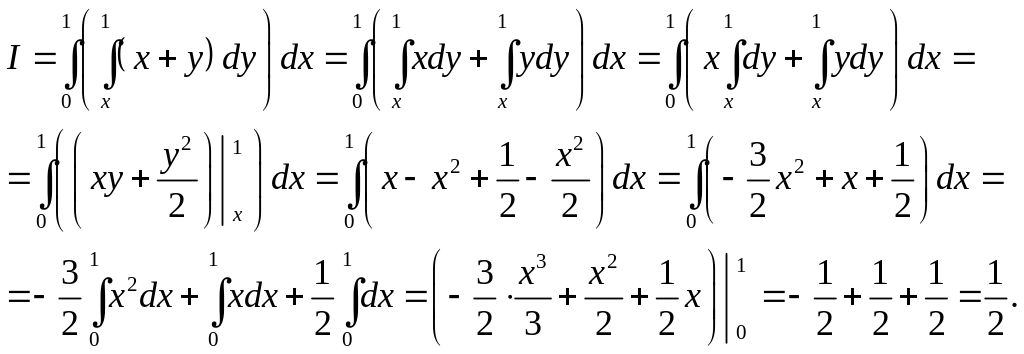
Пример 10.

Вычислить объем тела, ограниченного поверхностями , , , с помощью тройного интеграла.

Решение. Данное тело изображено на рис. 5. На рис. 6 изображена проекция этого тела на плоскость Оху.

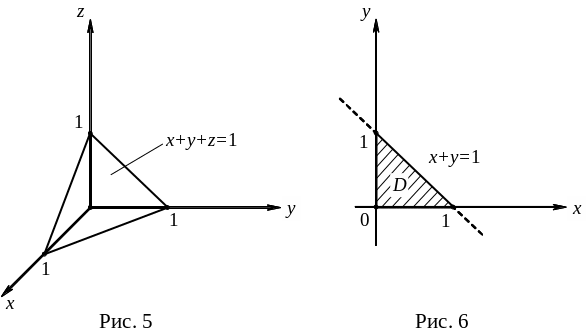
V= , где (V) – область, ограниченная поверхностями , , (координатные плоскости), (плоскость, отсекающая на координатных осях отрезки, равные 1), т. е. область (V) есть пирамида. Из чертежа видно, что по любой из переменных можно с одинаковым успехом брать постоянные пределы, и они равны 0 и 1. Возьмем, например, постоянные пределы по х ( ). Проекцией пирамиды на плоскость Оху является треугольник, ограниченный прямыми , и (рис. 6). Отсюда определяем пределы интегрирования по у ( ). Для переменой z нижним пределом будет, очевидно, (плоскость Оху), а верхним – значение z, полученное из уравнения плоскости

, т. е.

.

Определив пределы интегрирования по каждой переменной, можем представить данный тройной интеграл через повторный и вычислить объем тела:

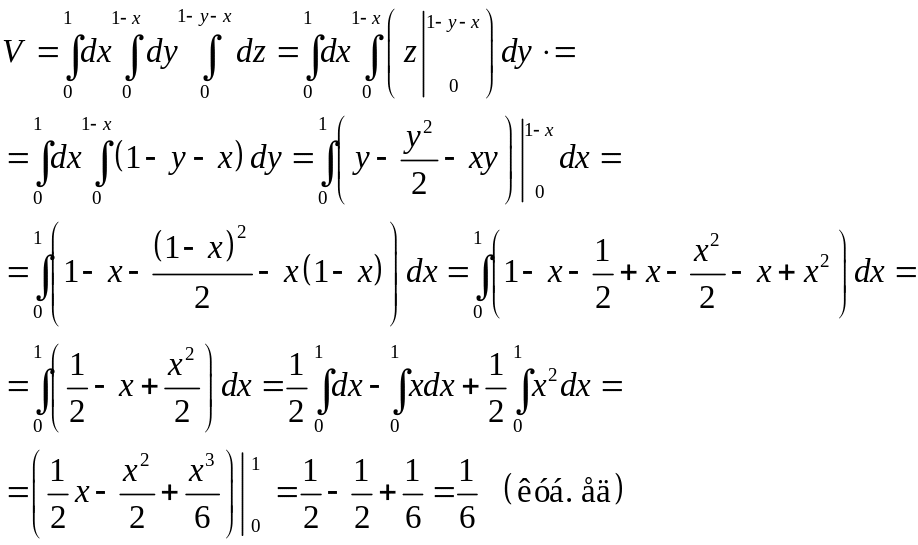
Пример 11. В первой урне 2 белых и 3 черных шара, во второй - 7 белых и 1 черный. Из первой урны в первую переложили 2 шара, затем наудачу извлекли шар из второй урны. Найти вероятность того, что выбранный из второй урны шар - белый.

Решение. Если событие А может произойти только совместно с одним из событий Н₁ , Н₂ , ..., Н , образующих полную группу несовместных событий (гипотез), то вероятность Р(А)появления события определяется по формуле полной вероятности: Р (А) = Р(H ) Р(А/H ), где Р(H ) - вероятность гипотезы H , Р(А/H ) - условная вероятность события А при этой гипотезе.

Вероятность извлечения белого шара из второй урны после добавления двух шаров из первой урны зависит от состава шаров (по цвету) в этой урне. При этом возможны следующие гипотезы:

Н₁ - из первой урны во вторую переложены два белых шара,

Н₂- из первой урны во вторую переложен один белый и один черный шар,

Н₃ - из первой урны во вторую переложены два черных шара.

Найдем вероятности этих гипотез . Вероятность каждой гипотезы связана с вероятностью извлечения соответствующих шаров из первой урны. Тогда получим

Р (Н₁ ) = = 0,1,

Р (Н₂) = = 0,6,

Р (Н₃) = = 0,3.

Пусть А - событие, состоящее в извлечении белого шара из второй урны, если предварительно имела место одна из гипотез Н_i. Условные вероятности события А будут :

Р(А/H₁) = 9/10, Р(A/Н₂) = 8/10, Р(A/Н₃) = 7/10.

По формуле полной вероятности найдем вероятность извлечения белого шара из второй урны

Р(А) = Р(H₁) Р(А/H₁) + Р(H₂) Р(А/H₂) + Р(H₃) Р(А/H₃) =

= 0,1 0,9 + 0,6 0,8 + 0,3 0,7 = 0,78.

Пример 12. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5, для третьего - 0,8. Мишень не поражена. Найти вероятность, что выстрелы произведены первым стрелком.

Решение. Если вероятности гипотез до опыта были Р (Н₁), Р (Н₂) , ..., Р(Н ), а в результате опыта появилось событие А , то условная вероятность Р(Н /A) с учетом появления события А вычисляется по формуле Бейеса:

Р(Н /A) =

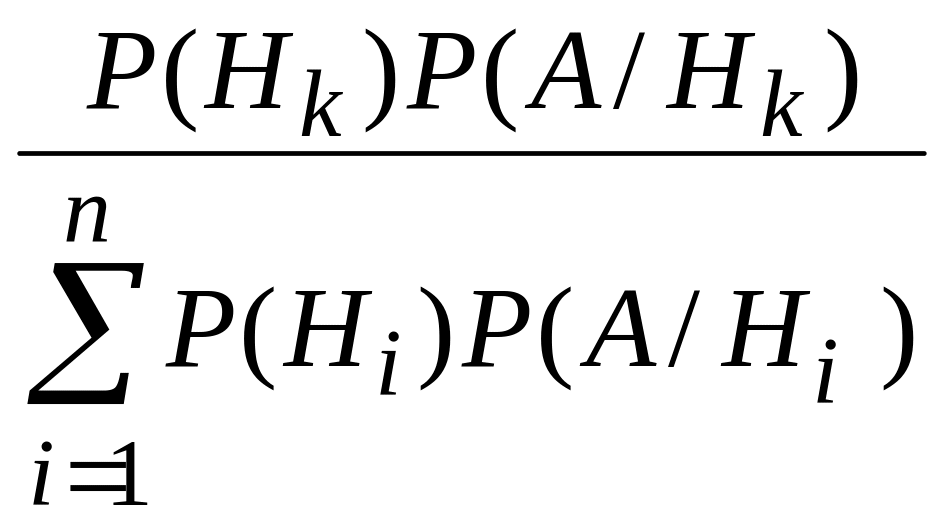
Возможны три гипотезы: H₁ - на линию огня вызван первый стрелок; H₂ - на линию огня вызван второй стрелок; H₃ - на линию огня вызван третий стрелок. Так как вызов на линию огня любого стрелка равновозможен, то вероятности этих гипотез до опыта Р(H₁) = Р(H₂) = Р(H₃) = 1/3.

В результате опыта наблюдалось событие А - после произведенных двух выстрелов мишень не поражена. Условные вероятности этого события

Р(А/H₁) = 0,7  0,7 = 0,49; Р(А/H₂) = 0,5  0,5 = 0,25; Р(А/H₃) = 0,2  0,2 = 0,04.

По формуле Бейеса для частного случая, когда вероятности гипотезы опыта равны между собой, находим вероятность гипотезы Н₁ после опыта:

Р(H₁/A) = = 0,628

Пример 13. Вероятность попадания в цель у стрелка р = 0,8. Производится три выстрела. Построить ряд распределения случайной величины Х – числа попаданий в цель. Найти математическое ожидание М [X] и дисперсию D [X].

Решение. Случайная величина Х может принимать значения : 0, 1, 2, 3. Вероятность того, что попаданий не будет р (х=0) найдем по формуле Бернулли P (k) = , здесь p = 0,8, q = 1- p= 0,2, n = 3, k = 0.

p (x=0) = = = 0,008.

Аналогично найдем p (x=1) – в результате трех выстрелов будет одно попадание

p (x=1)= = 0,8 0,4 = 0,096;

p (x=2)= 0,384; p (x=3)=0,512.

Ряд распределения будет иметь вид

x_i 0 1 2 3

p_i 0,008 0,096 0,384 0,512

Математическое ожидание М [Х] и дисперсию D [Х] определим по формулам

М [X] = х_ip_i =0,096 + 2 0,384 + 3 0,512 = 2,4 ;

D [X] = (х_i -M[X])² p _i ; или

D [X] = M[X²] – (M[X] )².

Предварительно построим ряд распределения случайной величины X²

x_i ² 0 1 4 9

p_i 0,008 0,096 0,384 0,512

M[X²] = 0,096 + 4 0,384 + 9 0,512 =6,24.

D [X]=6,24 – (2,4)² = 0,48.

Пример 14. Дана плотность распределения

f (x) =

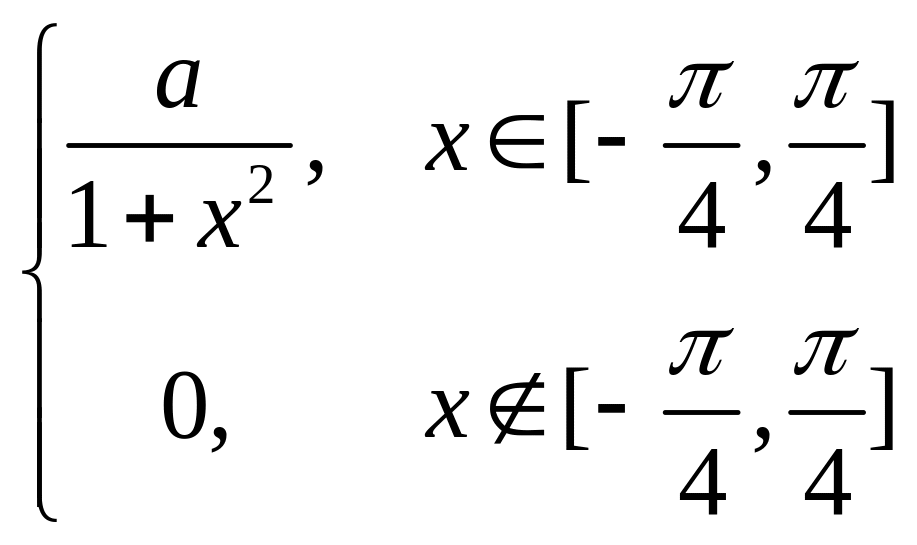
случайной величины Х. Найти параметр а, функцию распределения случайной величины, математическое ожидание М [X], дисперсию D [X], вероятность выполнения неравенства

0 < х< 3.

Решение. Для определения параметра а воспользуемся основным свойством плотности распределения

f (x) dx =1, т.к. при x плотность распределения равна нулю, то интеграл примет вид

dx =1, или

, откуда а =1/2.

Функция распределения связана с функцией плотности соотношением

F(x) = f (x) dx.

1) х< , F(x) = 0 dx=0;

2) x< , F(x) = 0 dx+ = ;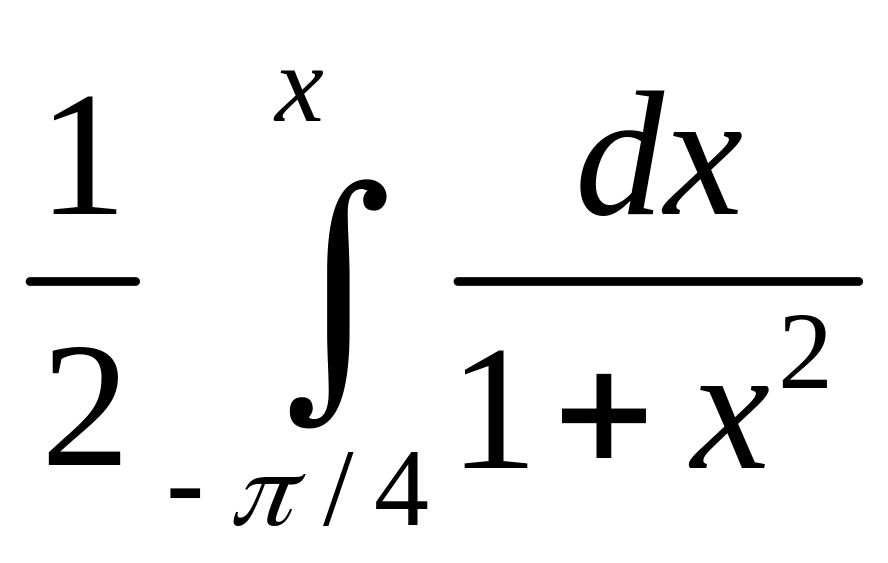

3) х F(x) = 0 dx+ +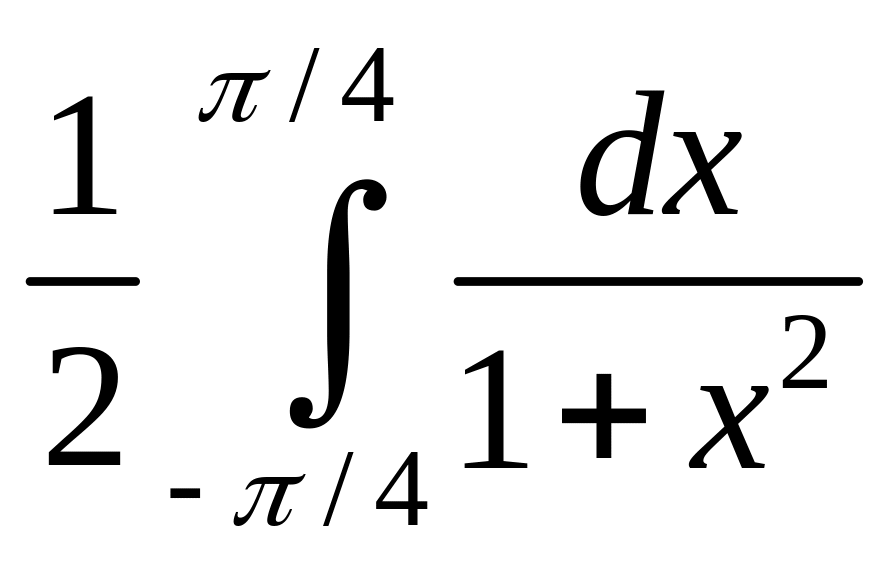

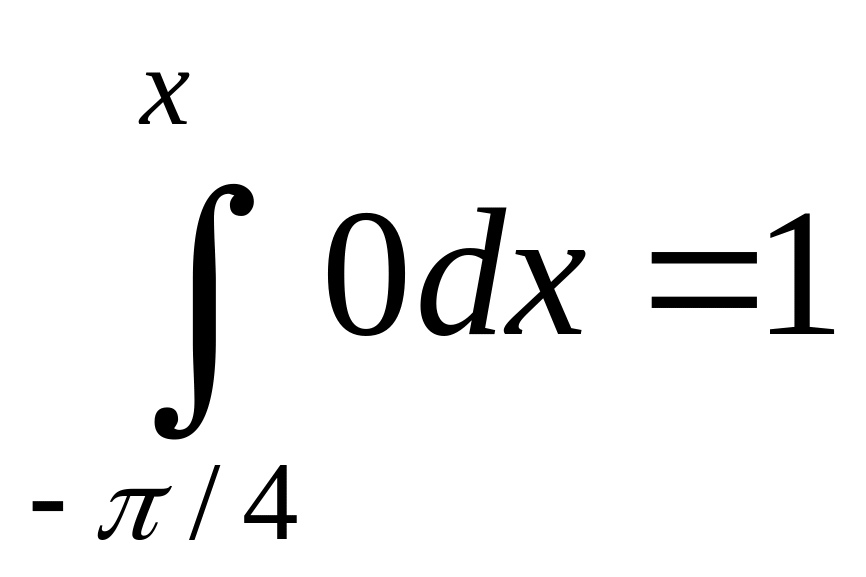
Таким образом F(x) =

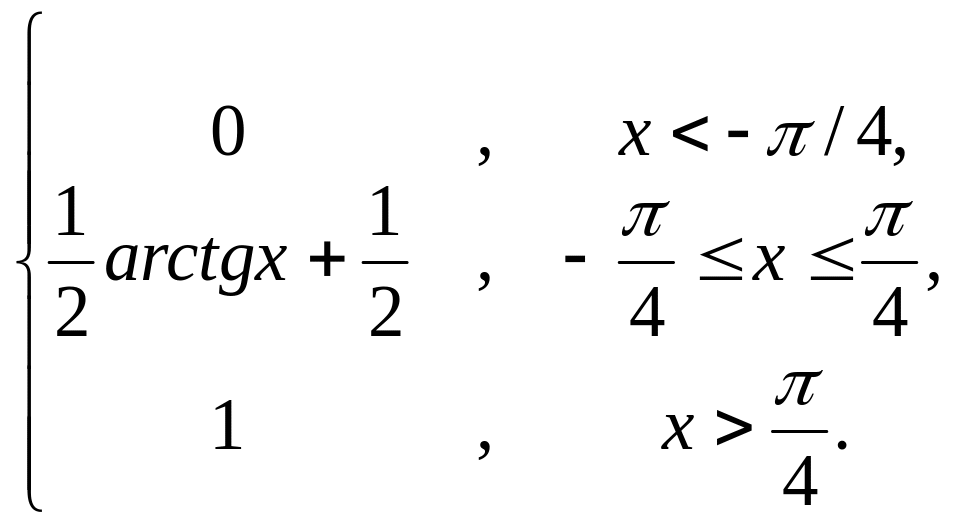
Математическое ожидание М [Х] и дисперсию D [Х] определим по формулам

М [X] = х f (x) dx, D [X] = (х -M[X])² f (x) dx

В нашем случае

М[X]= d x= = =0.

D [X] = dх = dх + = .

Вероятность выполнения неравенства 0 < х < определим по формуле

Р( 0 < х < ) = f (x) dx = F ( ) - F (0) = 1-1/2= 1/2.

Пример 15. Определить доверительный интервал для оценки с надежностью =0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, , если известно выборочное среднее = 14, объем выборки n = 25 и генеральное среднее квадратическое отклонение = 5.

Решение. Требуется найти доверительный интервал

-- < a < + (*)

Здесь t – значение аргумента функции Лапласа Ф (t). при котором 2 Ф (t)= . Все величины кроме t известны. Найдем t из соотношения Ф (t)= 0,95/2= 0,475. По таблице функции Лапласа, зная ее значение, находим значение аргумента t =1,96. Подставив t =1,96, = 5, n = 25, = 14 в (*), окончательно получим искомый доверительный интервал

12,04< a < 15,96.