1.2. Относительный покой (равновесие) жидкости

Здесь рассматриваются случаи относительного покоя жидкости, находящейся в сосуде, при движении в горизонтальном и вертикальном направлениях с постоянным ускорением  а и вращении цилиндрического сосуда вокруг вертикальной оси с постоянной угловой скоростью _о. Уравнения свободной поверхности при р=р_ат и начале координат, как показано на рис. 1.3, соответственно имеют следующий вид:

; (1.6)

Z_cв – Z₀ = h = 0; (1.7)

Z_cв – Z₀ = h = ₀²r²/(2g), (1.8)

где Z_cв – текущая координата поверхности жидкости в сосуде;

Z₀ – начальная глубина жидкости в сосуде для первых двух случаев или координата параболоида вращения.

Свободная поверхность жидкости для указанных выше случаев представляет собой соответственно наклонную к оси х под углом и горизонтальную плоскости, а также параболоид вращения. Для случая вращения жидкости в цилиндрическом сосуде из равенства объемов (см. рис.1.3, в) следует, что W_АВСD = W_ABEF – W_EOF, откуда легко выражается зависимость

h_пов = h_пон = 0,5h₀, (1.9)

где h_пов – повышение уровня жидкости у стенки сосуда над первоначальным уровнем;

h_пон – понижение уровня жидкости по оси сосуда под первоначальный уровень (см. рис. 1.3);

h₀ – высота параболоида вращения, соответствующая радиусу сосуда r₀.

Для первого и третьего случаев (см. рис. 1.3, а) давление в точке рассматриваемого объема жидкости определяется по уравнению (1.3), т.е. распределяется по гидростатическому закону, а глубину погружения точки под свободную поверхность жидкости рекомендуется определять по зависимости

h = Z₀ – Z  h. (1.10)

Для случая вращения жидкости в цилиндрическом сосуде величина h принимается всегда с положительным знаком. При вертикальном перемещении сосуда (рис. 1.3, б) с жидкостью с постоянным ускорением  а давление в точке рассматриваемого объема определяется по уравнению

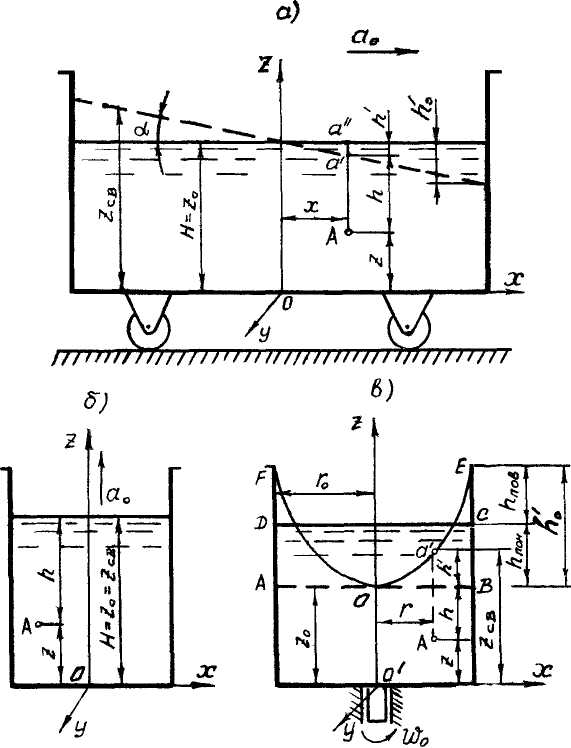
Рис. 1.3. Относительный покой жидкости: a – горизонтальное перемещение

сосуда с жидкостью; б – вертикальное перемещение сосуда с жидкостью;

в – вращение сосуда с жидкостью относительно вертикальной оси.

р = р₀ + (g  a)h, (1.11)

где знак вертикального ускорения зависит от его направления.

Общую методику решения задач по данной теме рассмотрим на примерах.

Пример 1.3. В цилиндрическую форму (рис.1.4) с внутренним диаметром D = 1120 мм и высотой l = 1000 мм залит цементный раствор для изготовления трубы центробежным способом. При толщине стенок цементной трубы у нижней и верхней грани соответственно ₁ = 60 мм и ₂ = 58 мм. Определить необходимую частоту вращения цилиндрической формы.

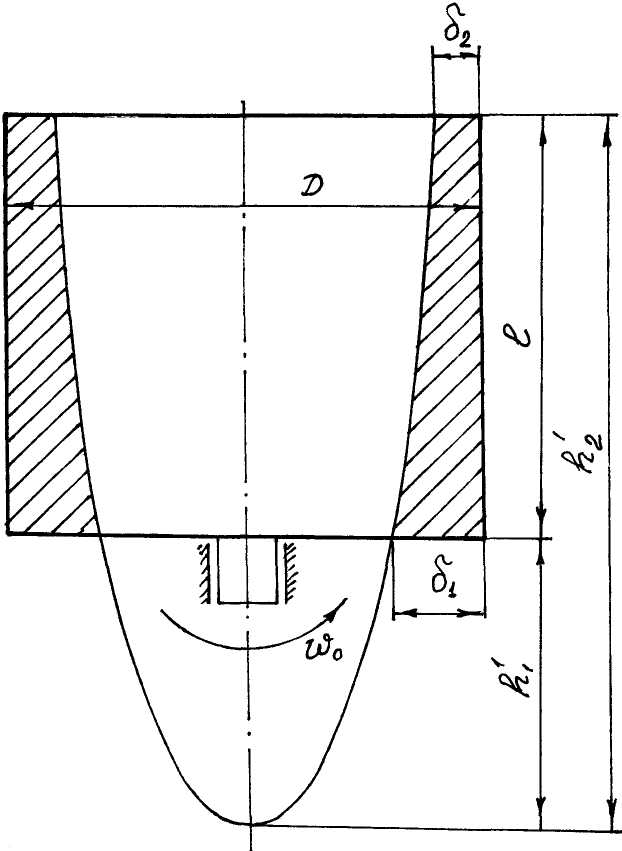
Рис. 1.4. Расчетная схема.

Решение. Определяется по (1.8) высота параболоида вращения h^₁ и h^₂ соответственно при r₁ = D/2 – ₁ = 1,12/2 – 0,06 = 0,500 м и r₂ = D/2––₁ = 1,12/2 – 0,058 = 0,502 м:

h^₁= ; h^₂= .

Из рис. 1.4 видно, что h^₂ – h^₁ = l = – (r₂²–r₁²).

Откуда определяется угловая скорость вращения цилиндрической формы:

Тогда частота вращения цилиндрической формы составит:

мин^–1.

Следует отметить, что при уменьшении частоты вращения цилиндрической формы толщина стенки ₂ цементной трубы будет уменьшаться, что является не всегда приемлемым.

Ответ: n = 15,76 с^–1 = 945,3 мин^–1.

Более полно решение задач по этой теме приводится в литературе [4, c.16, 17].