53)Преобразование фнч в режекторный фильтр

Поэтому, чтобы получить передаточную функцию режекторного фильтра из передаточной функции ФНЧ, нужно использовать следующее преобразование.

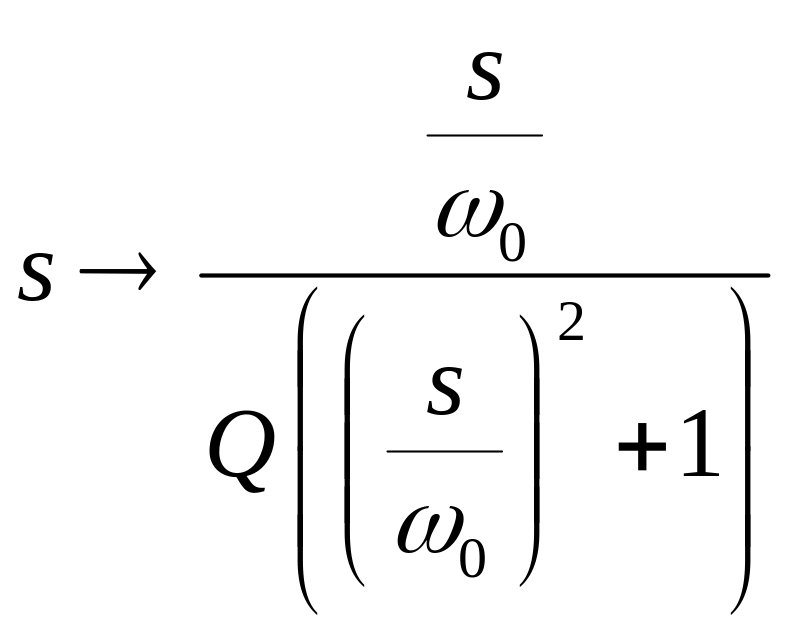Параметры преобразования связаны с нижней w₁ и верхней w₂ границами полосы задерживания полосового фильтра следующими соотношениями.

. Частоты нижней и верхней границ полосы задерживания полосового фильтра взяты равными следующим величинам w₁ =10рад/с и w₂ = 30рад/с.

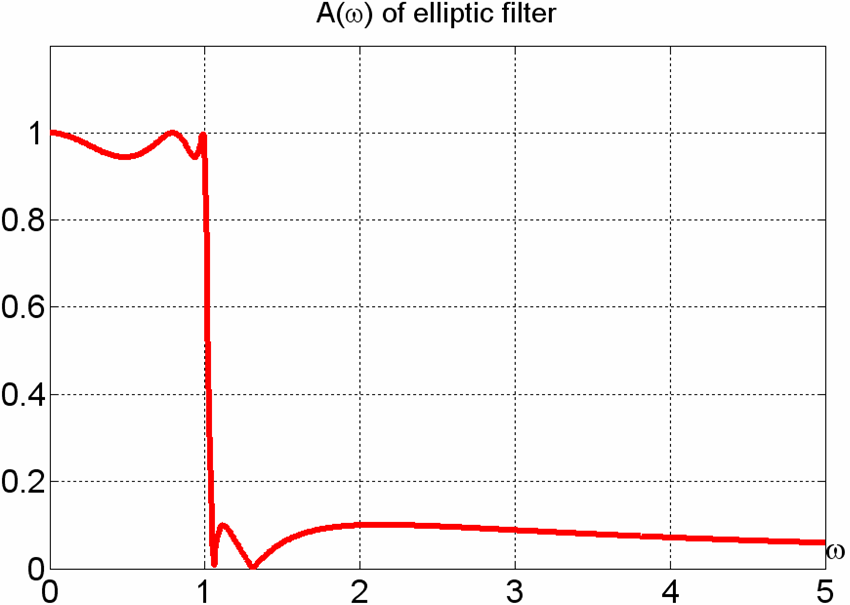
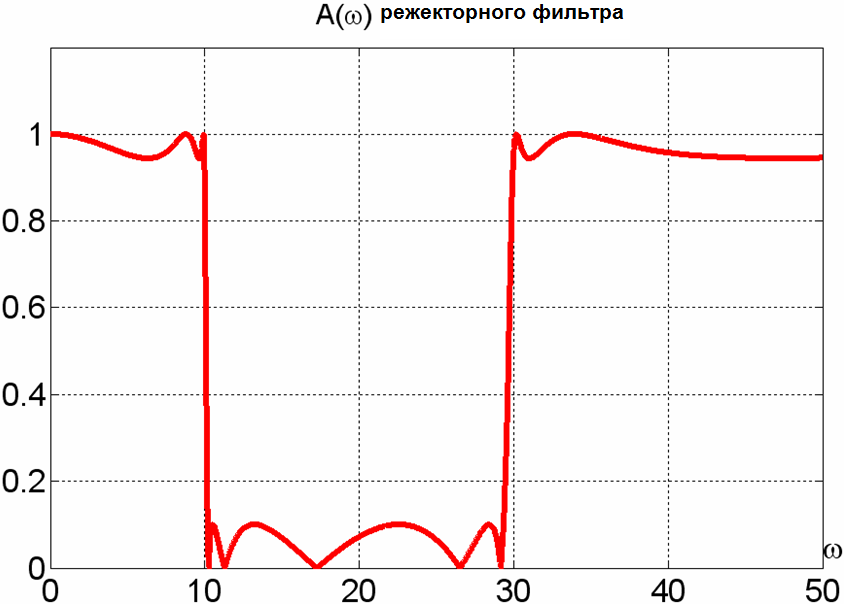
Из рисунков видно, что преобразование позволило получить из ФНЧ режекторный фильтр. Нули Im(z).

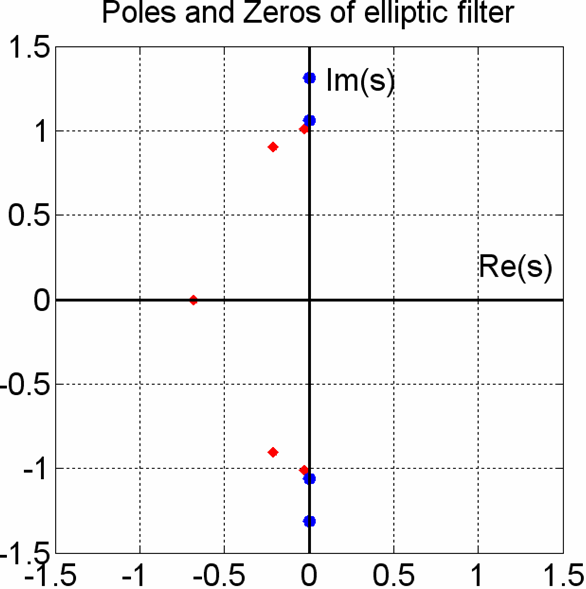
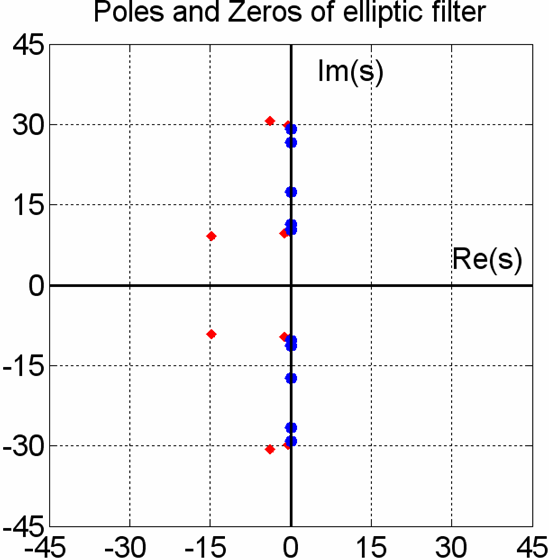
Первое, на что следует обратить внимание, это то, что изменилось число нулей и полюсов. Если внимательно рассмотреть рисунок, то можно увидеть 10 полюсов и 10 нулей. Второе, численные значения нулей и полюсов изменились.

54)Метод билинейного - преобразования

Данный метод позволяет синтезировать рекурсивный дискретный фильтр по частотной характеристике аналогового прототипа. В данном методе предлагается следующее билинейное преобразование .

Далее будем предполагать, что передаточные функции дискретного и аналогового фильтров связаны соотношением . Отсюда получаем искомую формулу перехода от аналогового фильтра-прототипа к дискретному фильтру . Частотная характеристика дискретного фильтра выражается через передаточную функцию следующим образом . Объединяя формулы получаем , а т.к. =>

=> Наконец используем связь между комплексным коэффициентом передачи и передаточной функцией аналогового фильтра .

Окончательно, объединяя формулы находим связь между частотными характеристиками дискретного и аналогового фильтров

Посмотрим на аргумент комплексного коэффициента передачи аналогового фильтра

. При малых значения аргумента тангенса, можно использовать приближенную формулу . Поэтому при низких частотах величина W будет равна

=>

Поэтому в области низких частот частотные характеристики аналогового и дискретного фильтров почти совпадают. Далее, по мере ускорения роста функции тангенса, частотная характеристика дискретного фильтра все сильнее сжимается по горизонтали (по сравнению с аналоговым прототипом).

55)Синтез нерекурсивных фильтров с использованием окон

Нерекурсивные фильтры – это фильтры без обратной связи. Нерекурсивные фильтры являются КИХ – фильтрами, т.е. имеют конечную импульсную характеристику. Нерекурсивные фильтры всегда устойчивы. Так как в основном уравнении дискретного фильтра обратные связи отсутствуют, то все коэффициенты a_m равны нулю m=0,1…

Поэтому передаточная функция нерекурсивного фильтра имеет следующий вид

(1). Передаточная функция выражается через импульсную характеристику (2). Сравнивая формулы (1) и (2) мы приходим к выводу, что сумма (2) является конечной суммой. Кроме того, элементы импульсной характеристики h(n) совпадают с коэффициентами b_n основного уравнения фильтра . Число N определяет порядок нерекурсивного фильтра. Таким образом, если порядок нерекурсивного фильтра равняется N , то его импульсная характеристика имеет N+1 отличных от нуля элементов.

Так как коэффициенты основного уравнения определяют конструкцию фильтра, то для синтеза нерекурсивного фильтра с заданной частотной характеристикой, необходимо знать нужную импульсную характеристику.

Таким образом, если мы имеем нерекурсивный фильтр порядка N, и нам известна импульсная характеристика h(n) , то частотную характеристику фильтра мы вычисляем с помощью суммы (3). Такая задача называется прямой задачей.

Синтез фильтра является обратной задачей. По заданной частотной характеристике K(f) и заданному порядку фильтра N , мы пытаемся подобрать элементы импульсной характеристики h(n) , такие, чтобы подстановка их в сумму (3) дала правильную частотную характеристику.

Увеличение порядка фильтра N означает увеличение электрических элементов в конструкции фильтра. Поэтому N является всегда конечным числом, большим или меньшим в зависимости от конструкции фильтра. Поэтому, используя конечное число элементов импульсной характеристики h(n) невозможно точно получить заданную частотную характеристику K(f) с помощью суммы (3).

Таким образом, сумма (3) может дать нам только приближенный результат. Поэтому задача различных методы синтеза фильтров состоит в выборе элементов импульсной характеристики, дающих лучший приближенный результат.

Метод окон является одним их таких методов синтеза нерекурсивных фильтров.

В основе этого метода лежит прямое и обратное преобразование Фурье дискретного сигнала. . Искомую частотную характеристику задаем в интервале от 0 до F , где F -частота Найквиста.