41)Частотная характеристика лдф

Определение. Частотная характеристика линейного дискретного фильтра – это комплексная функция K(w) действительного переменного w, и определяется соотношением: . Здесь w - это циклическая частота w = 2pf, а Dt – шаг дискретизации. Таким образом, чтобы найти частотную характеристику фильтра, надо в переходной функции сделать замену (1).

Вспомним, что передаточная функция H(z) является Z - образом импульсной характеристики h(n) фильтра . Поэтому передаточная функция и импульсная характеристика связаны друг с другом Z – преобразованием (2).

Заменяя в сумме (2) комплексную переменную z с помощью замены (1), получаем формулу для нахождения частотной характеристики фильтра.

Поэтому частотную характеристику можно представить в виде ряда (3). Если частотную характеристику фильтра рассматривать, как функцию обычной частоты f , то ряд (3) примет вид (4).

Спектр дискретного сигнала. Для аналогового сигнала s(t) выбирается шаг дискретизации Dt , и дискретный сигнал s_n находят по формуле

Затем спектр дискретного сигнала находят по формуле (5), здесь F - частота Найквиста .

Вспомним, что условие физической реализуемости ЛДФ накладывает на импульсную характеристику условие . Используя это условие, нижний предел суммирования в формуле (4) для частотной характеристики можно формально отодвинуть до - ¥ (минус бесконечности). Кроме того, в этой сумме заменим шаг дискретизации через частоту Найквиста. В результате получим:

Мы видим, что предыдущая формула для частотной характеристики ЛДФ, и формула (5) для спектра дискретного сигнала имеют одинаковую структуру. Поэтому, если импульсную характеристику h(n) рассматривать как дискретный сигнал, то частотная характеристика H( f ) будет равна спектру этого дискретного сигнала

H_D( f ), умноженному на удвоенную частоту Найквиста .

Так как частотная характеристика является спектром дискретного сигнала, то все свойства спектра дискретного сигнала, применимы к частотной характеристики ЛДФ.

Так, например, частотная характеристика является периодической функцией частоты с периодом 2F . . Кроме того, для вычисления частотной характеристики можно использовать дискретное преобразование Фурье ДПФ, и, в частности, быстрое преобразование Фурье БПФ.

42)Ких и бих фильтры

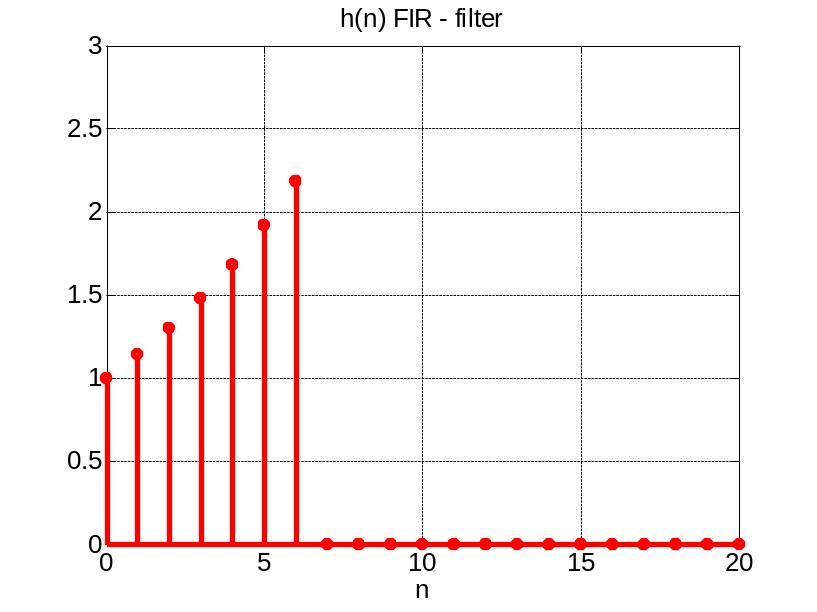
Конечной импульсной характеристикой ЛДФ будем называть импульсную характеристику, имеющую конечное число элементов отличных от нуля.

Другими словами, всегда существует такое число M , что для любого номера m большего M все элементы импульсной характеристики h(m) равны нулю. Фильтры с конечной импульсной характеристикой будем называть КИХ – фильтрами(FIR).

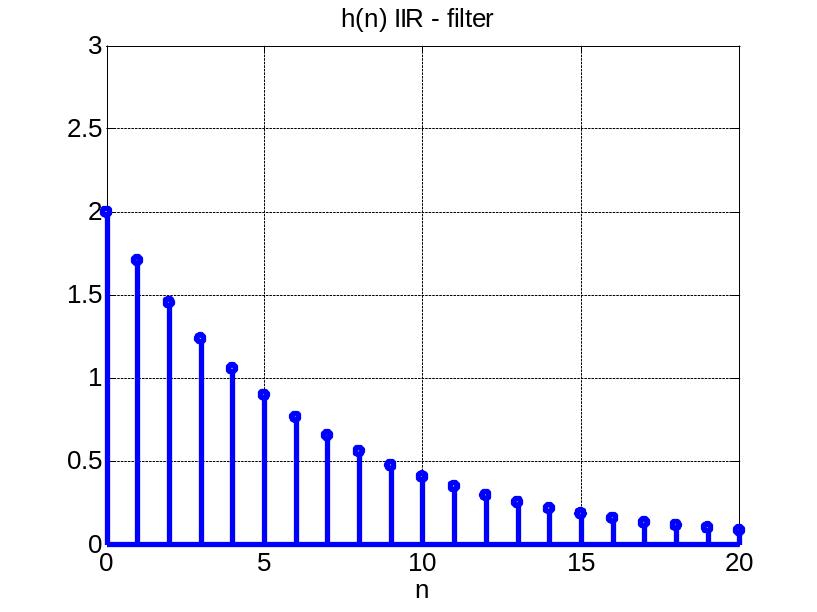
Бесконечной импульсной характеристикой ЛДФ будем называть импульсную характеристику, имеющую бесчисленное число элементов отличных от нуля.

Другими словами, какое бы большое число M мы не взяли, обязательно найдется такой номер m , для которого элемент импульсной характеристики h(m) будет отличен от нуля. Фильтры с бесконечной импульсной характеристикой будем называть БИХ – фильтрами(IIR).