38)Структурные схемы лдф. Прямая форма структурной схемы лдф

Линейный дискретный фильтр определяется своим основное разностным уравнением:

(1). Мы видим, что в уравнении присутствуют операции умножения на коэффициенты am , и bk операции задержки на m, n отсчетов. Поэтому схемы ЛДФ будем строить из двух простейших элементов.

Первый элемент осуществляет задержку на один отсчет. Уравнение такого элемента и его передаточная функция имеют следующий вид:

Второй элемент – умножитель осуществляет умножение на заданное число. Уравнение такого элемента и его передаточная функция имеют следующий вид:

Прямая форма структурной схемы ЛДФ

Прямая форма структурной схемы фильтра создается непосредственно по разностному уравнению фильтра. На рисунке показана структурная схема фильтра соответствующая уравнению

Далее отметим, что структурная схема может быть связана с передаточной функцией, если ее записать в виде:

39)Прямая каноническая форма лдф

Прямая каноническая форма – это структурная схема, содержащая минимальное количество элементов задержки. Для ее получения представим передаточную функцию (1)как результат последовательного соединения фильтров. Введем обозначения:

Тогда формула (1) примет вид: . Но такая запись, соответствует последовательному соединению фильтров с передаточными функциями H₁(z) и H₂(z). На рисунке показано последовательное соединение двух фильтров.

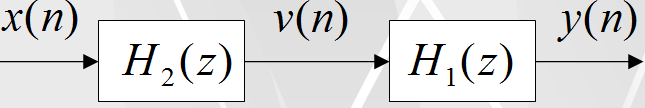
Для этих фильтров напишем соответствующие им разностные уравнения. У первого фильтра все коэффициенты a_m=0. Поэтому из общего разностного уравнения находим уравнение для первого фильтра: (2)

У второго фильтраb₀=1, а все остальные коэффициенты b_k=0. Поэтому из общего разностного уравнения находим уравнение для второго фильтра: (3)Структурная схема, соответствующая уравнениям (2), (3) показана на следующем рисунке.

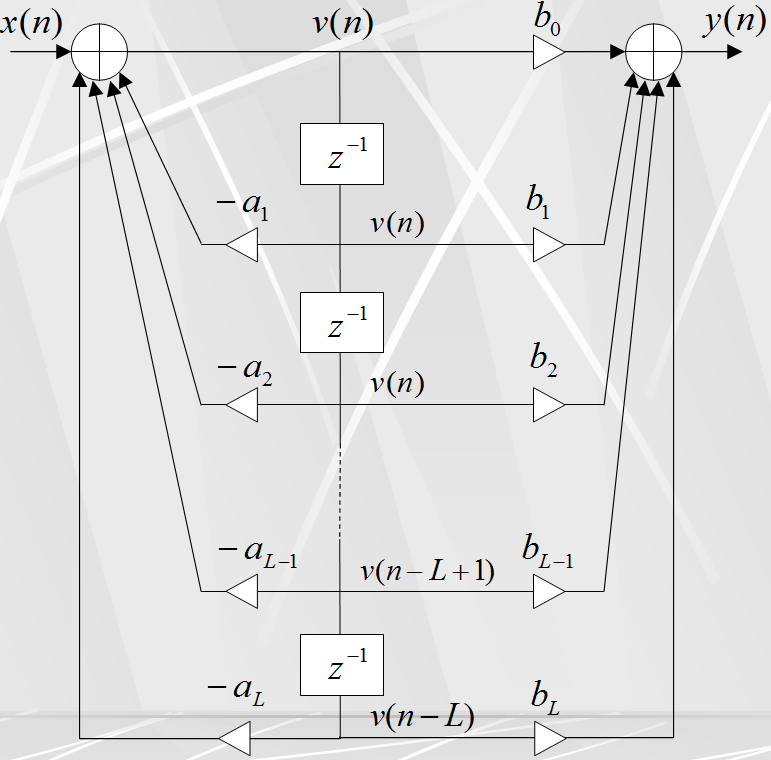
Здесь число L определяется по формуле:

40)Свойства линейных дискретных фильтров. Устойчивость лдф

Определение. Линейный дискретный фильтр называется устойчивым, если для любого ограниченного входящего сигнала |x(n)|≤C₁<∞, выходящий сигнал также ограничен

|y(n)|≤C₂<∞.

Необходимым и достаточным условием устойчивости ЛДФ, является выполнение условия: Здесь C - некоторая константа. Теперь мы посмотрим на проблему устойчивости линейного фильтра с другой точки зрения. Для выяснения устойчивости ЛДФ мы обратимся к передаточной функции H(z).

Для того чтобы ЛДФ был устойчив, необходимо и достаточно, чтобы все полюсы zn передаточной функции H(z) лежали в комплексной плоскости внутри единичного круга |z | < 1.

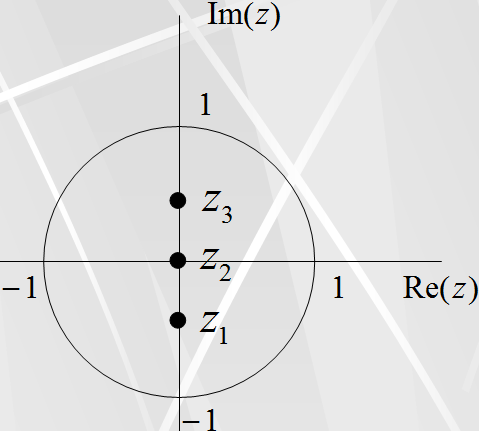
На первом рисунке показаны полюсы передаточной функции H1(z) первого фильтра. Полюсов три и все они находятся внутри единичного круга | z | < 1. Поэтому первый фильтр устойчив.

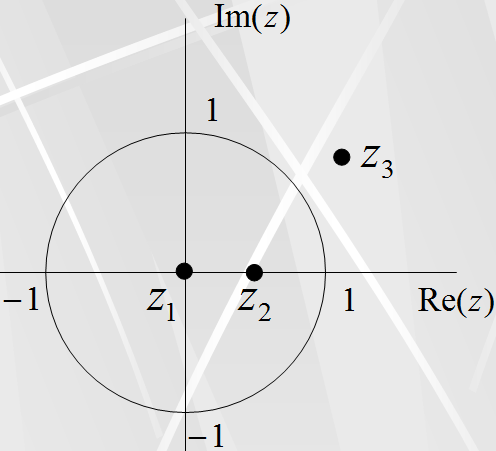
На втором рисунке показаны полюсы передаточной функции H2(z) второго фильтра. Полюсов тоже три, два из них z1, z2 лежат внутри единичного круга | z | < 1, а один полюс z3 вне единичного круга | z | ³ 1. Значит, второй фильтр неустойчив.