
- •1)Классификация сигналов по способу обработки, по физическим свойствам.
- •2)Спектральное представление сигналов
- •3)Ачх и фчх действительных сигналов
- •4)Примеры спектров некоторых сигналов
- •5) Прямоугольный импульс, задержанный во времени
- •6)Дуальность преобразования Фурье
- •7) Односторонний экспоненциальный импульс
- •8)Система функций Радемахера. Свойства
- •9) Система функций Уолша
- •10) Система функций Хаара
- •11)Тригонометрические ряды Фурье
- •12)Комплексная форма рядов Фурье
- •13)Спектральный анализ и преобразование Фурье
- •18)Спектр дискретного сигнала
- •19)Свойства спектра дискретного сигнала.
- •20)Спектральные свойства сигналов трех основных типов
- •21)Соотношение между спектрами непрерывного и дискретного сигналов
- •22)Теорема Котельникова
- •23)Дискретное преобразование Фурье
- •24)Свойства дискретное преобразование Фурье. Симметрия. Линейность
- •25)Свойства дискретное преобразование Фурье. Циклический сдвиг влево
- •26)Свойства дискретное преобразование Фурье
- •27)Быстрое преобразование Фурье (бпф)
- •28)Аналоговая обработка сигналов
- •29)Характеристики линейных систем
- •30)Условие физической реализуемости системы
- •31)Комплексный коэффициент передачи
- •32)Основное уравнение лпп системы
- •33)Нули и полюсы функция передачи системы
- •34)Z – преобразование
- •35)Обращение z – преобразования. Теорема о вычетах
- •36)Основное уравнение лдф и передаточная функция
- •37)Соединения линейных дискретных фильтров
- •38)Структурные схемы лдф. Прямая форма структурной схемы лдф
- •39)Прямая каноническая форма лдф
- •40)Свойства линейных дискретных фильтров. Устойчивость лдф
- •41)Частотная характеристика лдф
- •42)Ких и бих фильтры
- •43)Рекурсивные и нерекурсивные фильтры и их связь с ких и бих фильтрами
- •44)Аналоговые фильтры
- •46)Фильтр Чебышева первого рода
- •47)Три основных условия синтеза фильтров.
- •48)Фильтр Чебышева второго рода
- •49)Эллиптический фильтр
- •50)Преобразование фильтров. Изменение частоты среза фнч
- •51)Преобразование фнч в фильтр высокой частоты фвч
- •52)Преобразование фнч в полосовой фильтр
- •53)Преобразование фнч в режекторный фильтр
- •54)Метод билинейного - преобразования
- •55)Синтез нерекурсивных фильтров с использованием окон
- •56)Прямоугольное окно. Треугольное окно.
- •57)Окно Бартлетта. Окно Хана.
- •58)Окно Хэмминга. Окно Блэкмена.
- •59)Окно Кайзера. Окно Чебышева.
- •Цифровая обработка сигналов
35)Обращение z – преобразования. Теорема о вычетах
Пусть известно Z – преобразование X(z) бесконечной последовательности x(n) .
Тогда элементы
этой последовательности могут быть
найдены по ее Z
- образу X(z)
с помощью формулы.![]()
Здесь g - произвольный замкнутый контур лежащий в области аналитичности функции X(z) и охватывающий все ее особые точки. Кроме того, контур должен идти в положительном направлении, т.е. против часовой стрелки.
На рисунке показан g - контур, круг радиуса r , вне которого - образ является аналитической функцией.
Теорема о вычетах
Для вычисления интегралов (10) удобно использовать теорему о вычетах.
В курсе функций
комплексного переменного
доказывается следующая теорема
о вычетах.
Пусть f(z)
– аналитическая функция в некоторой
области D
, за исключением нескольких точек
, лежащих в этой области. Далее,
если g
- замкнутый контур, целиком лежащий в
области D
и охватывающий эти точки, то тогда
интеграл от функции f(z)
по контуру g
выражается через сумму вычетов
в этих точках.
![]() (1)
(1)
Вычеты
находятся с помощью следующих формул.
Пусть точка zk
- является полюсом
порядка
m
. Это означает, что функция f(z)
имеет вид:![]()
Здесь u(z) - аналитическая функция в области D . В этом случае вычет функции f(z) в точке zk находится взятием производной и переходом к пределу.
![]()
Чтобы использовать
теорему о вычетах
для вычисления интегралов (1), мы должны
функцию f(z)
заменить на следующую функцию.
![]()
36)Основное уравнение лдф и передаточная функция
Основное разностное уравнение линейного дискретного фильтра имеет вид.
![]() В
разностном уравнении переходим к Z
- образам. При этом учитываем свойство
задержки последовательности. В нашем
случае это приводит к следующим
соотношениям
В
разностном уравнении переходим к Z
- образам. При этом учитываем свойство
задержки последовательности. В нашем
случае это приводит к следующим
соотношениям
![]() .
В результате разностное уравнение
превращается в уравнение для Z
- образов.
.
В результате разностное уравнение
превращается в уравнение для Z
- образов.
![]() (1)
(1)
Решаем уравнение
(1).
В суммах (1)
Z
– образы выносим за знак суммы. Члены
с Y(z)
переносим налево, члены с X(z)
направо.
 (2)
(2)
Далее, из (2) получаем отношение Z – образов.
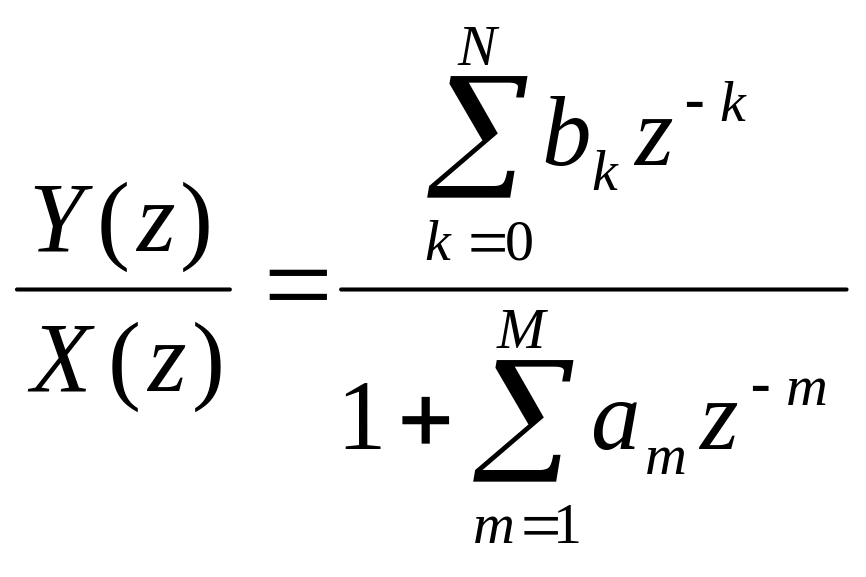 С
другой стороны, это отношение равно
переходной функции ЛДФ.
С
другой стороны, это отношение равно
переходной функции ЛДФ.
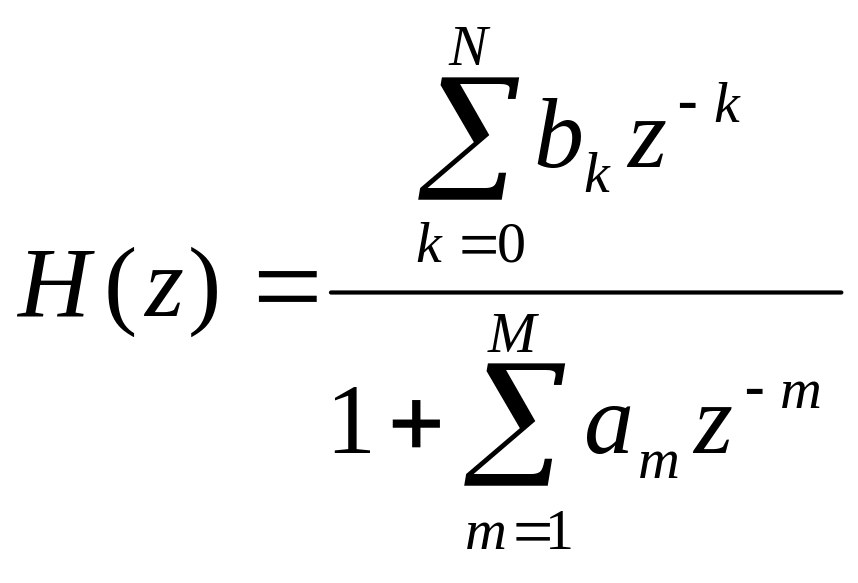 Таким
образом, мы получаем формулу, которая
позволяет вычислять
переходную функцию,
через коэффициенты
основного разностного уравнения ЛДФ.
Таким
образом, мы получаем формулу, которая
позволяет вычислять
переходную функцию,
через коэффициенты
основного разностного уравнения ЛДФ.
37)Соединения линейных дискретных фильтров
Последовательное соединение фильтров. Последовательное соединение фильтров показано на рисунке.
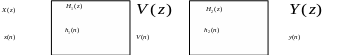
На вход системы из двух фильтров подается сигнал x(n), X(z) . На выходе имеем сигнал y(n), Y(z). Переходная функция системы фильтров определяется формулой.
![]() (1).
На каждом фильтре имеется входящий и
выходящий сигналы. Следую рисунку, для
них можно написать следующие соотношения.
(1).
На каждом фильтре имеется входящий и
выходящий сигналы. Следую рисунку, для
них можно написать следующие соотношения.
![]() (2).
Объединяя формулы (2)
получаем:
(2).
Объединяя формулы (2)
получаем:
![]() (3)
(3)
Подставляем (3)
в выражение
(1), и получаем
![]() .
Таким образом, при последовательном
соединении фильтров
передаточная функция системы равна
произведению
передаточных функций
фильтров.
.
Таким образом, при последовательном
соединении фильтров
передаточная функция системы равна
произведению
передаточных функций
фильтров.
Параллельное соединение фильтров.
В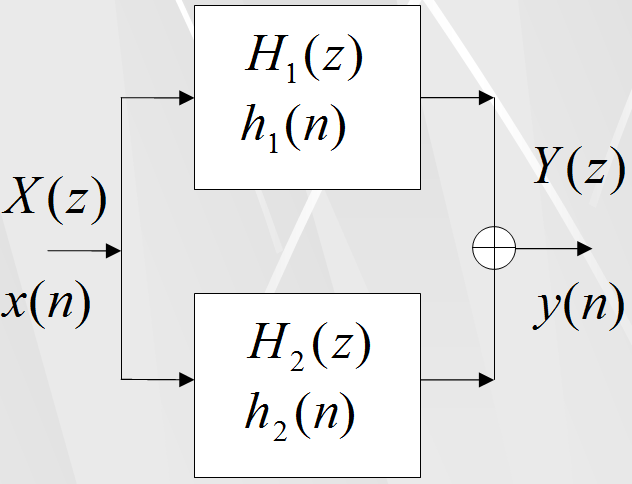 ходящий
сигнал X(z)
пройдя через каждый фильтр, преобразуется
в два сигнала:
ходящий
сигнал X(z)
пройдя через каждый фильтр, преобразуется
в два сигнала:
![]() (4)
(4)
Эти сигналы потом
складываются, образуя результирующий
сигнал.![]() (5)
(5)
Подставляя формулы (4) в сумму (5) получаем.
![]() (6)
(6)
Подставляем (6) в выражение (1), и получаем
![]()
