3.3.2. Свойства проводника, потерями в котором можно пренебречь

Динамические передаточные свойства проводника можно получить, пользуясь полным телеграфным уравнением. На практике обычно стремятся к тому, чтобы потерями в проводниках, и линиях связи можно было пренебречь. Поэтому случай проводника с пре­небрежимо малыми потерями особенно важен. Поло­жим вначале R'=0 и G'=0 (3.7) и получим для такого идеального проводника выра­жения

²U/z²= L'C'(²U/t²) (3.8)

²I/z²= L'C'(²I/t²) (3.9)

Ток и напряжение подчиняются волновому уравне­нию: волны тока и напряжения перемещаются вдоль проводника, не затухая, с фазовой скоростью:

(3.10)

Если в начале бесконечно длинного проводника (z = 0) подключен источник напряжения:

U_e(t)=U_e0()e^it, (3.11)

то волна напряжения, движущаяся в прямом направ­лении, описывается выражением:

U(z,t)=U_e0()e^i(t-z), (3.12)

Величину  = /v называют фазовой постоянной распространения. Для тока верно соотношение:

I(z,t)=I_e0()e^{i(t-z-)} (3.13)

В этом выражении появляется еще и сдвиг по фазе . Уравнение (3.1) связывает обе эти величины. Если подставить в него решения (3.12) и (3.13), то по­лучим =0 (5.51) Иными словами, ток и напряжение изменяются синфазно:

U(z,t)/I(z,t)= =Z₀ (3.14)

Для волны, распространяющейся в прямом направ­лении, отношение напряжения и тока постоянно и действительно в каждой точке проводника. Это отношение Z₀ называют волновым сопротивлением проводника, потерями в котором можно пренебречь. Таким образом, входное сопротивление бесконечно длинного проводника равно волновому сопротивлению. На самом деле каждый проводник имеет конечную длину l и подсоединен к полному сопротивлению Z_a.

1. Z_a – это сопротивление произвольного резистора или целой цепи различных элементов. На практике в результате этого волна, распространяющаяся в пря­мом направлении по проводнику, частично отражается с некоторым сдвигом по фазе . 0пределим комплексный коэффициент отражения

r = |r|e^i (3.15).

как отношение напряжений отраженной и падающей волн на выходном полном сопротивлении Z_а. Общие решения волновых уравнений (3.7) и (3.8) имеют вид

U=U₁e^i(t-z) + U₂e^i(t+z) (3.16)

I=I₁e^i(t-z) + I₂e^i(t+z) (3.17)

Выражения для четырех комплексных постоянных интегрирования U₁, U₂, I₁ и I₂ падающей и отражен­ной волн в этом случае можно получить с помощью уравнений (3.1), (3.11) и (3.16). Тогда получим:

U(z,t)=U_e0()[e^i(t-z) + re^{i(t+z-2l)}] (3.18)

I(z,t)=[U_e0()/Z₀][e^i(t-z) + re^{i(t+z-2l)}] (3.19)

Фаза (-2L) отраженной волны определяется конеч­ным временем пробега волны от конца проводника к точке z. Соотношение

Ua(t)=U(L,t)=Za∙I(l,t) (3.20)

вместе с уравнениями (5.56) и (5.57) позволяет вы­числить коэффициент отражения

r = (Za-Zo)/(Za+Zo) (3.21).

Это выражение справедливо и для проводников, по­терями в которых нельзя пренебречь (R'<>0,G'<>0), если полное сопротивление является комплексной ве­личиной [см. уравнение (3.27)].Для передачи сигналов наиболее важен случай, когда выходное полное сопротивление в точности равно волновому сопротивлению: Za = Zo.

2. В этом случае коэффициент отражения r=0 и отраженная волна не возникает. При этом входной сигнал без из­менений передается на выход линии. Возникает лишь запаздывание по времени 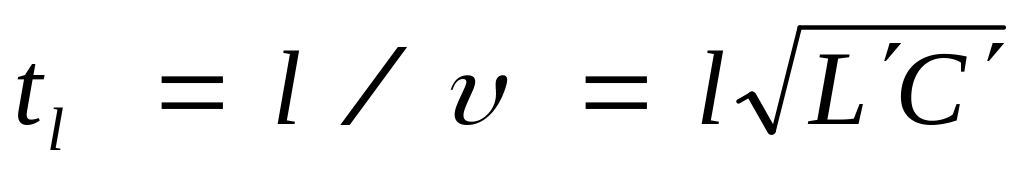(3.22) Выходной сигнал полностью поглощается в сопротив­лении Za. В этом случае говорят о том, что линия согласована (настроена).

3. В режиме короткого замыкания при Zа = 0 вели­чина коэффициента отражения r =-1. Иными сло­вами, волна напряжения полностью отражается с неизменной амплитудой, но со сдвигом по фазе на 180°.

4. Если же проводник присоединен к очень большому сопротивлению (режим холостого хода), то r=1. В этом случае волна напряжения полностью отражается с неизменной фазой. Происходит сложение волн: Ua(t)=2U_e0()e^i(t-l) (3.23) При этом на выходном сопротивлении возникает удвоенное напряжение. Для токов получаются проти­воположные соотношения [в соответствии с (3.20)]. Если линия не согласована, то следует учитывать и полное сопротивление генератора, подключенного к входу линии. Более подробное описание этого слу­чая можно найти в литературе [5.7, 5.10]. Теперь мы можем понять, почему искажается фор­ма сигналов на рис. 2. Если линия согласована (а), на экране осциллографа возникает правильный сиг­нал, повторяющий форму сигнала на выходе диода. Подсоединение проводника к высокоомному входу осциллографа (б) приводит к тому, что сигнал отра­жается со сдвигом по фазе; отражение повторяется на другом конце кабеля, поскольку фотодиод является генератором с высоким внутренним сопротивлением. В этом случае на выходе появляется повторный сиг­нал, запаздывающий по отношению к исходному на двойное время пробега сигнала вдоль кабеля. Длина кабеля и время запаздывания позволяют определить скорость распространения волн вдоль линии. Она со­ставляет примерно 20 см/нс (иными словами, 2/3 ско­рости света в вакууме с=3∙10⁸ м/с). Это значение характерно для большинства высокочастотных кабелей. Когда длина кабеля составляет 1 м (а), продолжительность импульса тока в диоде превышает удвоенное время пробега вдоль кабеля. Это приводит к дополнитель­ной модуляции сигнала. Нетрудно определить харак­теристики короткого несогласованного куска кабеля: он ведет себя как конденсатор с емкостью С'l (при­мерно 100 пФ), через который проходит импульс тока от фотодиода. Этот конденсатор разряжается с соот­ветствующими постоянными времени через входное сопротивление осциллографа и внутреннее сопротив­ление диода. Следует, конечно же, учитывать емкость диода и входного усилителя. Наблюдаемая постоян­ная времени порядка 10^-4 с хорошо согласуется с та­кой оценкой.