21. Линейные однородные диф. Ур-ния высших порядков и свойства их решений.

Линейным дифференциальным уравнением n-го порядка называют уравнение вида

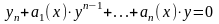
где функции a_i(x), непрерывны на некотором интервале i = (a;b)

существует решение ур-ния (1), удовлетворяющее начальным условиям y(x₀)*y₀; y’(x₀)*y’₀ ;y^n-1(x₀)*y₀^n-1 где х₀€ I, и это решение единственное.

Из этого утверждения следует, если решение 1 удовлетворяет нулевым начальным условиям y(x₀)=0; y’(x₀)=0 ; y^n-1(x₀)=0, то оно тождественно обращается в ноль на всем интервале I. Если ввести линейный оператор L(y)= yⁿ+a₁(x)*y^n-1+…+a_n(x)*y ,то L(y)=0

Свойство решений ур-ния (1):

1) Если у₁ и у₂ есть решение (1), то их сумма у₁+у₂ также есть решение (1) - это св-во следует из линейности оператора L(у₁ + у₂)=L( у₁)+L(у₂)=0+0=0

2) Если у – решение (1), то С*у , С=const, также реш-е (1) . L(Cy)=CL(y)=C*0=0

3) Если комплексно значная u(x)+i*v(x); (i²=-1 – линейная еденица) является решением ур-ния (1), то ее действительная часть u(x) и мнимая часть v(x) также являются решением ур-ния (1).

L(u(x)+i*v(x))=L(u(x))+i*L(v(x))=0; L(u(x))=0 и L(v(x))=0

Из св-в 1 и 2 следует, что множество решений ур-ния (1) обретает линейное пространство, поэтому для того, чтобы найти все решения (1) необходимо построить так называемую фундаментальную систему решений, т.е. ситему линейно независимых решений.

Напомним, что система ф-ций у₁(х), у₂(х)… у_n(х) является линейно независимой, если равенство α₁*у₁+ α₂*у₂+ α_n*у_n=0 (3) выполняется тогда и только тогда, когда все α_i=0 . Если же существует хотя бы одна из постоянных α_i-ых отличная от нуля при которой (3)имеет место, то системы функций у_1…у_n называют линейно зависимой.

Для установления линейной зависимости функций пользуются определителем Вронского:

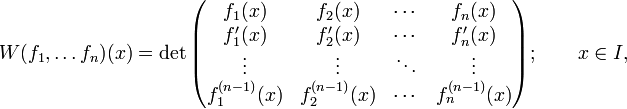
Имеет место утверждение: пусть у₁(х)…y_n(x) есть решение ур-ния (1), тогда а) если в некоторой точке х₀W(х₀)≠0 функции у₁(х)…y_n(x) – линейно независимы

б) Если существует хотя бы одна точка х₀ такая, что W(х₀)=0 , то ф-ция линейно зависима. Из этого условия следует, что определитель Вронского, составленный из фундаментальной системы решений, не образуется ни в одой точке интервала I.

22. Структура общего решения неоднородных линейных диф. Ур-ний высших порядков.

Рассмотрим линейное неоднородное дифференциальное уравнение y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x). Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянных C₁,..., C_n и удовлетворяющая следующим условиям: − при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ), x₀∈ [a;b], существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x, C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0}. Справедливо следующее утверждение (теорема о структуре общего решения линейного неоднородного уравнения). Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид y(x,C₁,..., C_n) = C₁y₁(x) + C₂y₂(x) + ... + C_ny_n(x) + y*(x), где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.

23. Линейная зависимость и независимость системы функций. Определитель Вронского. Линейные однородные диф. Ур-ния с постоянными коэффициентами. Характеристическое уравнение. Метод Эйлера.

Система функций y₁(x), y₂(x), …, y_n(x) называется линейно зависимой на интервале (a, b), если существует набор постоянных коэффициентов , не равных нулю одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a, b): для . Если равенство для возможно только при , система функций y₁(x), y₂(x), …, y_n(x) называется линейно независимой на интервале (a, b). Определитель Вронского (вронскиан) системы n - 1 раз дифференцируемых функций y₁(x), y₂(x), …, y_n(x) - определитель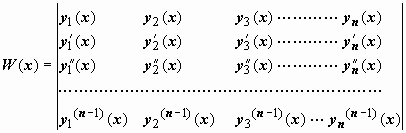

Теорема о вронскиане линейно зависимой системы функций. Если система функций y₁(x), y₂(x), …, y_n(x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.

Линейные однородные уравнения с постоянными коэффициентами

Рассмотрим уравнени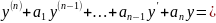е 0 (1), где 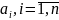- действительные числа. Будем решать ур (1) методом Эйлера. Согласно методу, решение ищем в виде (2), где - некоторый параметр. Продифференцируем (2) n раз и подставим в (1)

, ,…, .

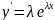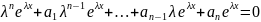
После деления на 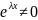получим 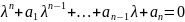(3)

Таким образом, для того чтобы (2) было решением (1) необходимо, чтобы удовлетворяло уравнению (3). Ур (3) называют характеристическим для (1). Рассмотрим следующие случаи

1. Пусть корни характеристического уравнения (3) различные действительные

Тогда согласно (2) каждому из этих корней будет соответствовать решение

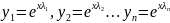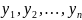. Легко показать, что определитель Вронского состоит из этих решений, например в точке х=0 отличен от 0, т.е. система решений линейно не зависимая, а значит, согласно теореме о структуре, общее решение в этом случае имеет вид:

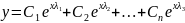, где С - произвольные постоянные.

2. Пусть среди корней ур. (3) есть комплексный 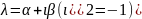. Т.к. коэффициенты уравнения (3) действительные, то обязательно есть комплексно сопряженный корень

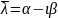. Пусть имеем пару Согласно формуле (2) имеем

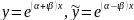
По формуле Эйлера представления комплексной экспоненты в тригонометрической форме будем иметь: .

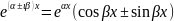Таким образом, паре комплексных сопряженных корней

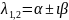
соответствует два решения

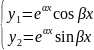. Легко показать, что функции 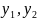- линейно не

зависимые.

А значит, общее решение в этом случае будет иметь вид:

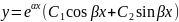
3. Пусть среди корней ур (3) есть действительный k кратный корень λ. Известно, что если λ - k кратный корень, то L(λ)=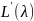 = 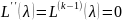; Пользуясь этим утверждением и используя формулу Ньютона-Лейбница дифференцируем произведения двух функций. Легко доказать, что k кратному действительному корню будет соответствовать k решений: 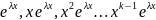. Общее решение

в этом случае имеет вид: .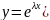

Если имеем kкратную комплексно-сопряженную пару (всего 2k корней). Общее решение имеет вид:

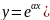
28. Основные понятия теории устойчивости по Ляпунову.

Пусть имеем систему дифференциальных уравнений

(1)

Решение системы (1), удовлетворяющее начальным условиям , называется устойчивым no Ляпунову при , если для любого существует такое, что для всякого решения , системы (1), начальные значения которого удовлетворяют условиям (2)

имеют место неравенства (3)

для всех .

Если при сколь угодно малом хотя бы для одного решения , неравенства (3) не выполняются, то решение называется неустойчивым.

Если, кроме выполнения неравенств (3) при условии (2) выполняется также условие (4)

то решение , называется асимптотически устойчивым.

Исследование на устойчивость решения , системы (1) можно свести к исследованию на устойчивость нулевого (тривиального) решения , некоторой системы, аналогичной системе (1),

27. Линейные неоднородные системы диф. Ур-ний с постоянными коэф.

Рассмотрим систему (1)

А – действительная матрица, f(x) – вектор-функция.

Если в (1) f(x) имеет специальный вид

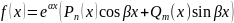то, частное решение, в случае отсутствия резонанса, находится по тем же правилам, что и для неоднородного уравнения.

Если пара α±iβ встречается k-раз то, в частном решении вместо множителя x^kвозникают многочлены на k единиц больше чем самая большая степень многочленов правой части.

1) α±iβ – не корень 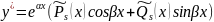S=max(m,n)

2) α±iβ –k корень кратности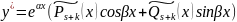

Метод вариации заключается в нахождении n–неизвестных функций C₁(x),…C_n(x). При нахождении общего решения системы уравнений производится замена постоянных С₁,…С_n на соответствующие функции C₁(x),…C_n(x). Составляется система из n – уравнений из, которой находим эти неизвестные. После подставляем найденные выше C₁(x),…C_n(x) в общее решение и получаем ответ.

26. Линейные однородные системы диф. Ур-ний с постоянными коэф. Характеристическое уравнение. Метод Эйлера.

Рассмотрим систему (1)

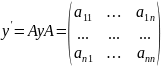– действительная матрица.

Согласно методу Эйлера решение системы (1) будем искать в виде 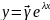(2) λ – некоторый параметр, γ – числовой вектор

Дифференцируя (2) и подставив в (1) получим

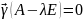(3); Е – единичная матрица.

Система (3) является линейной однородной алгебраической системой относительно неизвестного вектора γ. Для того, чтобы эти системы имели ненулевое решение необходимо чтобы её главный определитель был равен 0. Т.е. 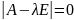(4)

Характеристическое уравнение для данной системы имеет вид

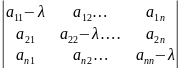(4)

Пусть среди корней (4) есть комплексно-сопряжённые λ_1,2α±iβ. Согласно формуле Эйлера будем иметь:

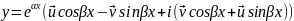
По свойствам решений системы (1) решениями будут

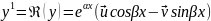
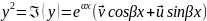
25. Линейные неоднородные диф. Ур-ния с постоянными коэф. Метод вариации произвольных постоянных.

Рассмотрим систему (1)

А – действительная матрица, f(x) – вектор-функция.

Если в (1) f(x) имеет специальный вид

то, частное решение, в случае отсутствия резонанса, находится по тем же правилам, что и для неоднородного уравнения.

Если пара α±iβ встречается k-раз то, в частном решении вместо множителя x^k возникают многочлены на k единиц больше чем самая большая степень многочленов правой части.

1) α±iβ – не корень S=max(m,n)

2) α±iβ –k корень кратности

Метод вариации.

Заключается в нахождении n–неизвестных функций C₁(x),…C_n(x). При нахождении общего решения системы уравнений производится замена постоянных С₁,…С_n на соответствующие функции C₁(x),…C_n(x). Составляется система из n – уравнений из, которой находим эти неизвестные. После подставляем найденные выше C₁(x),…C_n(x) в общее решение и получаем ответ.

2. Пусть правая часть (1) имеет вид f(x)=P_m(x)e^αx тогда

1)Если α – не является корнем характеристического уравнения, то частное решение имеет вид y*=Q_m(x)e^αxQ_m(x) –многочлен m-ой степени с неопределенными коэф.

2) Если α является к- кратным корнем характеристического

уравнения, то y*=x^kQ_m(x)e^αxQ_m(x),

3. Пусть F(x) имеет вид f(x)= P_m(x)*cos(βx)+Q_l(x)*sin(βx)

1) Если пара +αβ не является корнем характеристического уравнения, то частное решение ищется в виде M_s(x)*cos(βx)+N_s(x)*sin(βx) , где M_s(x) , N_s(x) – многочлен со степенью S с неопределенным коэф. Причем S=max(m,l).

2)Если +αβ является к-кратной пары корней характеристического уравнения, тогда решения ищутся в виде

y*=x^k(M_s(x)*cos(βx)+N_s(x)*sin(βx))

4. f(x)= e^αx (P_m(x)*cos(βx)+Q_l(x)*sin(βx)), тогда

1)Если +αβ не является корнем характеристического уравнения, частные решения имеют вид y*=x^k(M_s(x)*cos(βx)+N_s(x)*sin(βx))

2)Если +αβ к-кратная пара корней характеристического уравнения, тогда решение имеет вид y*=x^ke^αx(M_s(x)*cos(βx)+N_s(x)*sin(βx))

Если правая часть (1) представляет собой линейную комбинацию перечисленных выше функций, то для нахождения общего решения применяют принцип суперпозиции.

24. Линейные неоднородные диф. Ур-ния с постоянными коэф. И специальной правой частью.

Рассмотрим уравнение y⁽ⁿ⁾+a₁y ^(n-1)+…+a_n-1y^’+a_ny=f(x) (1), где a_i, i=1,n; a_i – действительные числа. Если в (1) f(x)-любая непрерывная функция, то (1) интегрируется методом вариации произвольных постоянных.

Если в (1) f(x) имеет специальный вид ,то f(x)=e^αx(P_m(x)*cos(βx)+Q_l(x)*sin(βx)), P_m(x), Q_l(x)- m,l–полиномы соответственных степеней, то частные решения (1) ищутся методом подбора (методом неопределенных коэффициентов).

Рассмотрим некоторые частные случаи.

1. Пусть первая часть (1) представляет собой многочлен некоторой степени (m). F(x)=P_m(x)=A₀x^m+A₁x^m-1+…+A_m-1x+A_m, тогда

1) Если 0 не является корнем характеристического уравнения λⁿ+a₁λ^n-1 +…+a_n-1λ+a_n=0, то частное решение y* для (1) также ищем в виде многочлена (m) степени с неопределенным коэф.

y*=B₀x^m+B₁x^m-1+…+B_m-1x+B_m

Для того, чтобы найти коэф. B_i, i=0,m дифференцируем y* n-раз. Затем подставляем y*,y*’…y*⁽ⁿ⁾ в (1) и приравниваем в полученном соотношении слева и справа коэф. при x^m, x^m-1 ,…,x⁰.

Из полученной системы находим B₀, B₁,… Общее решение системы (1) – y=y₀+y*

2) Если 0 –является k- кратным корнем характеристического уравнения, то частное решение в этом случае ищут в виде y*=x^k(B₀x^m + B₁x^m-1+…+B_m-1x+B_m). Коэф. B_i находится описанным выше способом. Этот случай называется резонансным.