
- •1. Числовой ряд и его сумма. Необходимое условие сходимости ряда. Критерий Коши сходимости ряда.
- •2. Достаточные условия сходимости ряда: признаки сравнения, признаки Даламбера и Коши, интегральный признак.
- •3. Знакочередующиеся ряды, признак Лейбница. Абсолютная и условная сходимость.
- •4. Функциональные ряды, сумма ряда, область сходимости. Равномерная сходимость функциональных рядов. Признак Вейерштрасса.
- •5. Непрерывность суммы функционального ряда. Почленное дифференцирование и интегрирование функционального ряда.
- •6. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда.
- •7. Непрерывность суммы степенного ряда. Почленное дифференцирование и интегрирование.
- •8. Ряды Тейлора. Теорема о единственности разложения. Разложение некоторых элементарных функций в ряд Маклорена.
- •9. Применение рядов к решению диф. Уравнений, вычисление определённых интегралов (некоторые применения степенных рядов).
- •10. Тригонометрический ряд Фурье. Достаточное условие сходимости.
- •11. Ряд Фурье для функций с периодом 2π, для функций с произвольным периодом. Тригонометрический ряд Фурье в комплексной форме.
- •12. Интеграл Фурье. Косинус- и синус- преобразование Фурье и их свойства. Комплексная форма интеграла Фурье.
- •13. Основные понятия теории дифференциальных уравнений. Общее и частное решения.
- •18. Общие понятия о диф. Ур-ниях высших порядков. Задача Коши. Теорема существования и единственности решения задачи Коши.
- •19. Уравнения, допускающие понижения порядка.
- •20. Понятие о краевых задачах. Линейная краевая задача.
- •21. Линейные однородные диф. Ур-ния высших порядков и свойства их решений.
- •22. Структура общего решения неоднородных линейных диф. Ур-ний высших порядков.
- •23. Линейная зависимость и независимость системы функций. Определитель Вронского. Линейные однородные диф. Ур-ния с постоянными коэффициентами. Характеристическое уравнение. Метод Эйлера.
- •28. Основные понятия теории устойчивости по Ляпунову.
- •27. Линейные неоднородные системы диф. Ур-ний с постоянными коэф.
- •26. Линейные однородные системы диф. Ур-ний с постоянными коэф. Характеристическое уравнение. Метод Эйлера.
- •25. Линейные неоднородные диф. Ур-ния с постоянными коэф. Метод вариации произвольных постоянных.
- •24. Линейные неоднородные диф. Ур-ния с постоянными коэф. И специальной правой частью.
- •29. Устойчивость по Ляпунову решений линейных систем второго порядка.
- •30. Устойчивость нелинейных систем по первому приближению.
- •31. Фазовая плоскость и особые точки двумерных систем.
- •32. Преобразование Лапласа и его свойства. Оригинал изображения. Линейность, подобие, изображение свёртки. Формулы обращения преобразования Лапласа. Теоремы разложения.
- •34. Классификация уравнений математической физики.
- •33. Применение преобразования Лапласа к решению диф. Ур-ний и систем, уравнений в частных производных.
- •39. Уравнения Лапласа. Решение задачи Дирихле в круге методом Фурье.
- •40. Метод сеток для решения уравнений математической физики.
- •37. Метод Фурье решения волнового уравнения.
- •36. Вывод основных уравнений математической физики: колебания струны, теплопроводности.
- •35. Приведение линейных уравнений в частных производных второго порядка к каноническому виду.
- •38. Метод Даламбера решения уравнений математической физики.
8. Ряды Тейлора. Теорема о единственности разложения. Разложение некоторых элементарных функций в ряд Маклорена.
Известно, что для любой ф-ции f(х) определенной в окрестности точки А, имеющие в ней производные до (n+1) порядка включительно, справедлива формула Тейлора f(x)= f(a)+f’(a)/1!+f’’(a)/2!*(x-a)2+fn(a)/n!*(x-a)n+rn(x) где
rn= f(n+1)ƺ(x-a)(n+1)/(n+1)!это соотношение записываем в виде f(x)=Pn(x)+rn(x), где Pn(x)- многочлен тейлора
если ф-ция f(x)-бесконечно дифференцируемая в окрестности точки А и остаточный член rn(x)(n→∞) стремится к 0 , то из ф-лы Тейлора получаем разложение ф-ции f(x) по степеням (х-а) называемые рядом Тейлора.
Теорема о разложении функции в ряд Тейлора. Если функция w = f(z) аналитична в области D, z0 ∈ D, то функция f(z)может быть разложена в ряд Тейлора по степеням (z – z0)n. Этот ряд абсолютно сходится к f(z) внутри круга | z – z0| < r, где r - расстояние от z0 до границы области D (до ближайшей к z0 точке, в которой функция теряет аналитичность). Это разложение единственно.
Единственность разложения следует из того, что коэффициенты ряда однозначно выражаются через производные функции
f(x)= f(a)+f’(a)/1!+f’’(a)/2!*(x-a)2+fn(a)/n!*(x-a)n если (а)=0, то называют рядом Маклорена.
Разложение основных ф-ций в ряд Маклорена имеет вид:
![]()
![]()
![]()
![]()
![]()
![]()
9. Применение рядов к решению диф. Уравнений, вычисление определённых интегралов (некоторые применения степенных рядов).
1) Приближённое вычислениее значений ф-ции.
Для
приближённого вычисления ф-ции f(x)
в ее разложении в степенной ряд
сохраняются первые n
членов, а остальные отбрасываются. Для
оценки погрешности полученного
приближения требуется оценить сумму
отброшенных членов
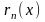 .
В случае Лейбницевского ряда используется
оценка
.
В случае Лейбницевского ряда используется
оценка
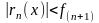 где
где
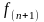 -
первый из отброшенных членов ряда. Если
исходный ряд знакопостоянен, то ряд
составляется из отброшенных членов,
сравнивают с бесконечно убывающей
прогрессией.
-
первый из отброшенных членов ряда. Если
исходный ряд знакопостоянен, то ряд
составляется из отброшенных членов,
сравнивают с бесконечно убывающей
прогрессией.
2) Приближенное вычисление определённых интегралов.
Применяют
в случае, когда первообразное не
выражается через элементарные ф-ции.
Если при вычислении интеграла
 с точностью до Ɛ, подинтегральная ф-ция
f(x)
разлагается по степеням х в интервале
сходимости (-R;R)
- этот интервал включает в себя отрезок
[a;b],
то используют св-ва почленного
интегрирования этого ряда. Ошибка
вычислений определяется также как и
при вычислении значений ф-ции, т.е. как
b(а).
с точностью до Ɛ, подинтегральная ф-ция
f(x)
разлагается по степеням х в интервале
сходимости (-R;R)
- этот интервал включает в себя отрезок
[a;b],
то используют св-ва почленного
интегрирования этого ряда. Ошибка
вычислений определяется также как и
при вычислении значений ф-ции, т.е. как
b(а).
3) Интегрирование дифференциальных уравнений с помощью рядов.
Будем рассматривать в основном интегрирование линейных диф. уравнений

Если
коэффициент
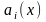 i=0..2
и функция f(x)
- является аналитическими функциями,
т.е. разлагаются на некотором интервале
(а,b),
в степенные ряды, то решение (1) ищут в
виде степенного ряда y(x)=
i=0..2
и функция f(x)
- является аналитическими функциями,
т.е. разлагаются на некотором интервале
(а,b),
в степенные ряды, то решение (1) ищут в
виде степенного ряда y(x)=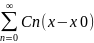 (2) .Если же коэф. уравнения (1)
или f(x)
имеют особые точки, то решение уравнения
(1) ищут в виде обобщенного степенного
ряда y(x)=
(2) .Если же коэф. уравнения (1)
или f(x)
имеют особые точки, то решение уравнения
(1) ищут в виде обобщенного степенного
ряда y(x)=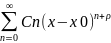 где
где
 любое действительное число.
любое действительное число.
13
14
15
19
10. Тригонометрический ряд Фурье. Достаточное условие сходимости.
Тригонометрическая система функций
Функция y = f (x) , определенная на множестве X , называется
периодической с периодом T > 0, если при каждом x €X значение
(x- T), (х+ Т) €X и выполняется равенство f(x ±T) = f(x) .
Отметим, что для построения графика периодической функции
периода T достаточно построить его на любом отрезке длины T и
периодически продолжить на всю область определения X .
Тригонометрической системой функций называется система
cos х, sinх , cos2х , sin2х , , cosnx, sinnx,. (1)
Система функций (1) периодична с периодом 2p .
Свойства системы (1):
1) Интеграл по отрезку [- п; п] от произведения двух различных
функций равен нулю (свойство ортогональности).
2) Интеграл по отрезку [-п;п ] от квадрата любой функции из
(1) равен п.
Тригонометрический ряд Фурье — представление произвольной функции f с периодом τ в виде ряда
|
Достаточное условие сходимости ряда Фурье.
Если
f
– суммируемая функция и при фиксированном
х и некотором
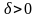 интеграл
интеграл

существует, то частичные суммы Sn ряда Фурье функции f сходятся в этой точке х к f(x).
11. Ряд Фурье для функций с периодом 2π, для функций с произвольным периодом. Тригонометрический ряд Фурье в комплексной форме.
Ряд Фурье функции с произвольным периодом
Предположим, что функция f задана в промежутке [-l,l], где l -- некоторое положительное число. Сделав подстановку
![]()
получим функцию
![]() ,определенную
в промежутке
,определенную
в промежутке
![]() . Функции g соответствует (формальный)
ряд Фурье
. Функции g соответствует (формальный)
ряд Фурье
![]()
коэффициенты которого находятся по формулам Эйлера -- Фурье:
![]()
![]()
Возвращаясь
к старой переменной, т.е. полагая в
выписанных формулах
![]() ,
мы получим для функции f тригонометрический
ряд несколько измененного вида:
,
мы получим для функции f тригонометрический
ряд несколько измененного вида:
![]()
где
![]()
![]()
Ряд Фурье для функций с периодом 2π
Периодическая функция f (x) с периодом T = 2π допускает представление в виде ряда Фурье
![]()
коэффициенты которого определяются формулой
![]()
Выражение
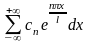 называется комплексной формой ряда
Фурье функции f(x), если
называется комплексной формой ряда
Фурье функции f(x), если
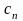 определяется равенством
определяется равенством
![]()
где
![]()
Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:
