1. Числовой ряд и его сумма. Необходимое условие сходимости ряда. Критерий Коши сходимости ряда.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Рассматриваются числовые ряды двух видов: вещественные числовые ряды, комплексные числовые ряды.

Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.

Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда представляют собой либо вещественные, либо комплексные числа.

Ряд u1 + u2 + u3 + ... + un + ... может сходиться лишь в том случае, когда член un (общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.

Критерий Коши: Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.

Критерий Коши сходимости ряда: для того чтобы последовательность чисел (действительных или комплексных) хn, n=1, 2, . . ., имела предел, необходимо и достаточно, чтобы для любого существовал такой номер N, что для всех выполнялось неравенство

2. Достаточные условия сходимости ряда: признаки сравнения, признаки Даламбера и Коши, интегральный признак.

1. Признак сравнения.

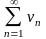Ряды и – положительные.

а) Если члены данного ряда , начиная с некоторого номера, меньше членов ряда и ряд сходится, то данный ряд сходится.

б) Если члены данного ряда , начиная с некоторого номера, больше членов ряда и ряд расходится, то данный ряд расходится.

Замечание 1. Если члены ряда больше членов ряда и ряд сходится, признак не применим.

Замечание 2. Если члены ряда меньше членов ряда и ряд расходится, признак не применим.

Замечание 3. При использовании признаков сравнения надо знать ряды, с которыми можно сравнить данный ряд. К ним относятся:

1) ряды 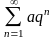, которые составлены из членов бесконечной геометрической прогрессии; при эти ряды сходятся, при расходятся;

2) – ряд Дирихле, при сходится, при 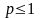расходится.

2. Предельный признак сравнения.

Если существует конечный и отличный от нуля , то два ряда и одновременно сходятся или расходятся.

3. Признак Даламбера.

Дан положительный ряд .

Если , то при ряд сходится, при – расходится, при признак не применим.

1

2

4

5

6

3