3.7 Диффузия в прямоугольное окно

При проведении локальной диффузии, которая проводится в планарной технологии, например, при формировании диффузионных резисторов, при формировании эмиттеров и ряда других областей. При этом остальная часть поверхности пластины защищена маской, чаще всего из SiO₂, которая выполняет роль отражающей границы.

Пусть источник примеси представляет собой прямоугольник размером 2а x 2b (рис. 3.7).

Если источник неограниченной, обеспечивающий в бесконечно тонком приповерхностном слое постоянную концентрацию примеси , решение записывается в виде:

(3.35)

Рис. 3.7. Диффузии в прямоугольное окно

Если по поверхности распределение равномерное с плотностью Q

(3.36)

Здесь, как и ранее, .

При локальной диффузии примесь мигрирует как перпендикулярно поверхности пластины, так и под край маскирующего окисла, так как процесс диффузии в кремнии изотропен. Обычно считают диффузию под край окисла на расстояние 0,8-1,0 x_j слоя.

3.8. “Разгонка” примеси. Многостадийная диффузия

Как уже отмечалось, перераспределение примеси идет в процессе выполнения всех высокотемпературных операций, следующих после введения примеси. Если перед началом какой-то операции имелся Гауссов профиль распределения примеси, а последующая операция проводится при той же температуре, то, очевидно, профиль распределения останется Гауссовым, но с измененной величиной характеристической длительности диффузии, т.е. в соответствующей формуле будет фигурировать сумма времен, описывающего исходный профиль (t₁) и последующей операции (t₂). В общем случае, если температуры были разными, то нужно суммировать соответствующие .

Если исходный профиль не Гауссов, то для вычисления результирующего профиля следует использовать формулу Пуассона. В частности, если на стадии загонки был сформирован профиль, описываемый erfc- функцией, то формула Пуассона запишется в следующем виде:

(3.37)

Здесь соответствует стадии “загонки”, а – последующей “разгонке” или сумме всех последующих высокотемпературных процессов, в ходе которых идет перераспределение примеси.

Если в несколько раз превышает , то получающийся профиль будет мало отличаться от Гауссова с характеристической величиной = + .

При обратном соотношении, которое иногда выполняется при формировании эмиттера, профиль распределения приблизительно описывается erfc-функцией, в которой также должна фигурировать суммарная величина и, соответственно, уменьшенная величина ( _эфф), поскольку общее количество примеси (при отражающей границе) остается неизменным.

Q определяется из формулы:

(3.38)

При изготовлении многослойных структур разгонку примесей часто совмещают с окислением, используемым для формирования диффузионной маски из SiO₂ (см. далее).

3.9. Диффузия примеси в гетерогенной системе

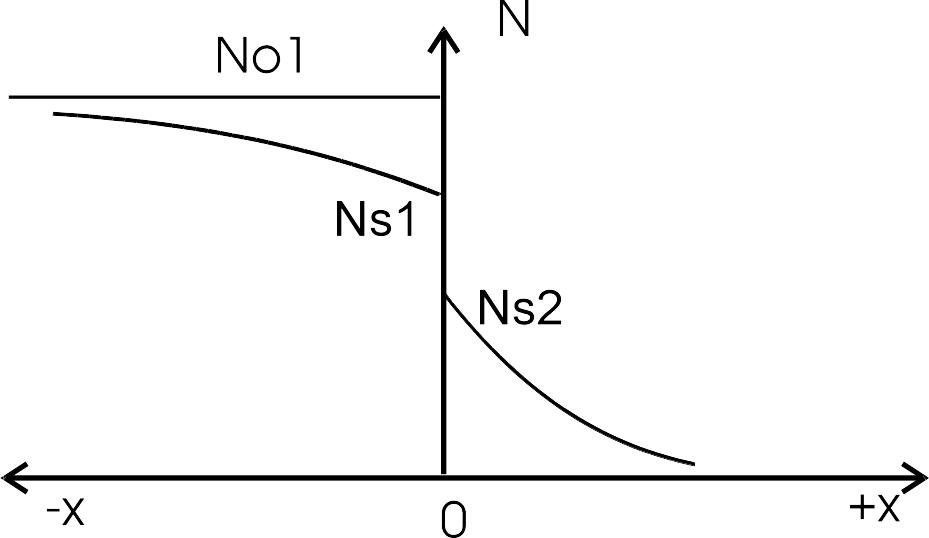
Рассмотрим этот случай на примере двух полубесконечных тел, имеющих контакт по плоскости. Одно из них содержит примесь в концентрации No1. Для гетерогенной системы используется понятие коэффициента распределения примесей (С), характеризующего отношение концентраций примеси на плоскости контакта тел (рис. 3.8).

(3.39)

Рис. 3.8. Диффузии в гетерогенной системе

При этом выполняется условие равенства потоков по обе стороны границы раздела тел. Если бы профили распределения в обоих телах описывались erfc-функциями, то это второе условие согласно формуле (3.26), записывалось бы в форме:

(3.40)

Из уравнений (3.39) и (3.40) можно найти , и получить окончательные выражения для профилей распределения примесей:

; (3.41)

; (3.41)

(3.42)

Предположение о том, что профили распределения примесей описываются erfc-функциями, подтверждается более аккуратными расчетами. Эта ситуация достаточно типична для случаев легирования полупроводника из нанесенного на ее поверхность слоя.