6. Конечные разности.

Определение 1.Пусть - сетка узлов, - значения функции f(x) в узлах

: значения называются разделенными разностями нулевого порядка функции f(x) : значения называются разделенными разностями первого порядка функции f(x). : значения называются разделенными разностями второго порядка функции f(x).. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . : значения называются разделенными разностями n–го порядка функции f(x).

Простейшие свойства разделенных разностей.1.f(x₀, x₁, …, x_k) – симметричная функция своих аргументов, т.е. не меняется при любой перестановке аргументов.

Заметим, что любая разделенная разность есть линейная функция своих аргументов.

f(x₀, x₁, …, x_k) = . (устанавливается по индукции) => результат.

2.Если f(x)=P_n(x) – многочлен n-ой степени, то разделенные разности порядков  (n+1) равны нулю.

Заметим, что P_n(x, x₀) многочлен (n-1)-ой степени,

P_n(x, x₀, x₁) многочлен (n-2)-ой степени,

………………………………………………

P_n(x, x₀, x₁, …, x _n-1) - многочлен 0-ой степени (т.е. const),

P_n(x, x₀, x₁, …, x _n)  0.

………………………………………………

7.Интерполяционный многочлен Ньютона.

Рассмотрим многочлен n-ой степени вида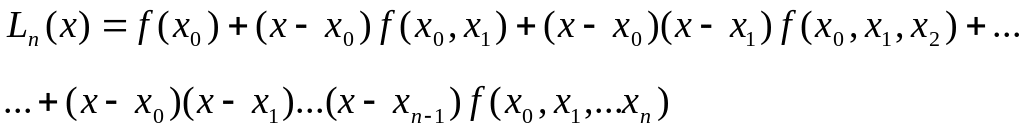 (9)

Теорема 3.Многочлен (9) является интерполяционным для f(x) на сетке узлов , т.е. , i=0, 1,…, n (10)

Рассмотрим разделенные разности многочлена Лагранжа : . (11)

Числитель в (11) – многочлен n -ой степени, обращающийся в 0 в т. . Следовательно, по теореме Безу числитель в (11) делится без остатка на , а, следовательно, -многочлен (n-1) -ой степени.

Из (11) находим . (12) Далее . (13) Числитель в (13) – многочлен степени (n-1) обращается в 0 при ,следовательно, делится на без остатка,  L_n (x, x₀, x₁) - многочлен (n-2)-ой степени.Из (12) с учетом (13) находим

. (14)

Продолжая таким же образом далее и учитывая, что (n+1) - ая разделенная разность

L_n(x, x₀, …, x_n)  0, окончательно находим

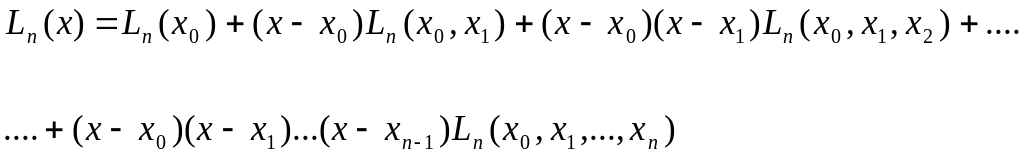(15)

Но по условию теоремы - интерполяционный многочлен для f(x) , т.е. , i=0, 1,…, n .Следовательно, все разделенные разности для и f(x) совпадают, поэтому (15) можно переписать

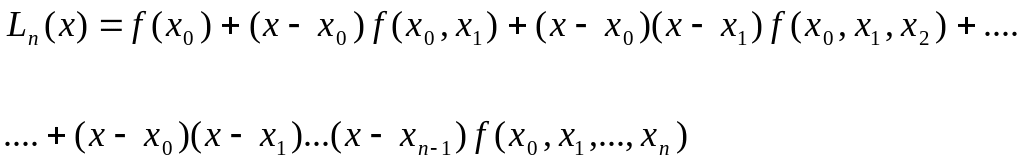(16)

т.е. получаем представление (9), что и требовалось доказать.

Замечание 1.Мы получили другую форму представления интерполяционного многочлена Лагранжа. Многочлен (9) называется интерполяционным многочленом Ньютона и обозначается также - .

Замечание 2.Интерполяционный многочлен в форме Лагранжа содержит значения в явном виде. Это удобно, когда необходимо построить интерполяционный многочлен на тех же узлах, но для другой функции – g(x). Тогда значения достаточно заменить на .Многочлен в форме Ньютона содержит неявно (через разделенные разности).Однако, он удобен, когда для той же функции f(x) необходимо увеличить порядок n. Тогда к исходному многочлену достаточно добавить несколько членов стандартного вида.