Прогнозирование сезонных явлений

Пример. В таблице 1.5 представлены данные, характеризующие количество продукции, проданное компанией “Lewplan plc” в течение последних 13 кварталов. Необходимо проанализировать эти данные и установить, можно ли обнаружить тенденцию. Если устойчивая тенденция действительно существует, то данную модель можно использовать для прогнозирования проданной продукции в следующие кварталы.

Таблица 1.5 Количество проданной продукции

Дата	Номер квартала	Объем продаж, тыс. шт.
Январь – март 19х6 Апрель – июнь Июль – сентябрь Октябрь – декабрь Январь – март 19х7 Апрель – июнь Июль – сентябрь Октябрь – декабрь Январь – март 19х8 Апрель – июнь Июль – сентябрь Октябрь – декабрь Январь – март 19х9	1 2 3 4 5 6 7 8 9 10 11 12 13	239 201 182 297 324 278 257 384 401 360 335 462 481

По данным таблицы 1.5 с помощью Мастера диаграмм построен график

изменения объема продаж (рис.9).

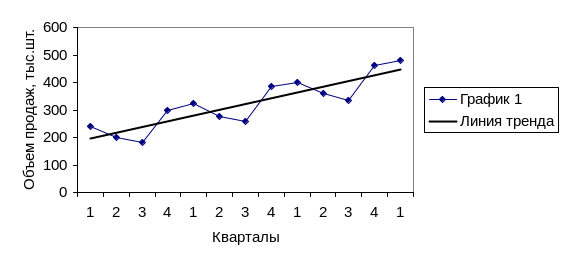Рис. 9. Объемы продаж компании “Lewplan plc” по кварталам

в натуральном выражении

Как следует из графика, возможен возрастающий тренд, содержащий сезонные колебания. Объемы продаж в зимний период (кварталы 1 и 4) значительно выше, чем в летний (кварталы 2 и 3 ). Амплитуда сезонных колебаний практически не изменяется в течение трех лет. Этот факт говорит в пользу модели с аддитивной компонентой, которая может быть представлена следующим образом:

У = Т + S + Е,

где У – фактическое значение объема продаж,

Т – трендовое значение,

S – сезонная вариация,

Е – ошибка (случайная составляющая).

В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения, т.е. значения сезонной компоненты увеличиваются (или уменьшаются) с возрастанием значений тренда. Тогда строится мультипликативная модель, составляющие которой записываются в виде сомножителей.

В моделях, как с аддитивной, так и с мультипликативной компонентами, общая процедура анализа и прогноза включает следующие этапы:

1. Расчет значений сезонной компоненты.

2. Исключение сезонной компоненты из фактических наблюдений (десезонализа-

ция) и моделирование тренда на основе полученных данных.

3. Проверка точности модели

4. Прогнозирование.

Этап 1. Для расчета значений сезонной компоненты воспользуемся методом четырехзвенной (четыре квартала в году) скользящей средней. Просуммировав первые четыре значения и разделив полученную сумму на 4, определим средний объем продаж в каждом квартале 19х6 года:

(239 + 201 + 182 + 297 ) / 4 = 229,75.

Полученное значение уже не содержит сезонной компоненты, так как представляет собой среднюю величину за год. У нас появилась оценка значения тренда для середины года, то есть для точки, лежащей между кварталами 2 и 3. Если последовательно продвигаться вперед (т. е. отбросить первое наблюдение, равное 239 и, добавив следующее – 324, разделить сумму на 4 и т. д.), то можно рассчитать средние квартальные значения на промежутке: апрель 19х6 – март 19х7 (251), июнь 19х6 – июль 19х7 (270,25) и т. д. Данная процедура позволяет генерировать скользящие средние по четырем точкам для исходного множества данных. Получаемое таким образом множество скользящих средних представляет оценку искомого тренда.

Рассчитанные значения тренда можно использовать для нахождения оценок сезонной компоненты: У – Т = С + Е, но прежде следует скользящие средние центрировать, чтобы они относились к тем же временным интервалам, что и исходные данные. Так, первая оценка, равная 229,75, представляет собой точку, совпадающую с серединой 19х6 года, т.е. лежит в центре промежутка фактических объемов продаж во 2 и 3 кварталах. Вторая оценка, равная 251, лежит между фактическими значениями в 3 и 4 кварталах. Нам же требуются десезонализированные средние значения, которые можно было бы сравнить с фактическими. Найдем среднюю из первой и второй оценок, центрируя их на июль – сентябрь 19х6 г., т.е. (229,75 + 251 ) / 2 = 240,4, которую можно непосредственно сравнивать с фактическим значением за этот период, равным 182. Результаты этих расчетов приведены в таблице 1.6.

Таблица 1.6 - Расчет центрированных скользящих средних значений

тренда для модели У – Т = S + Е по четырем точкам

Дата	Объем продаж, тыс.шт.	Скользящая средняя за 4 квартала	Центрированная скользящая средняя	Оценка сезонной компоненты У – Т = S+Е
Январь-март 19х6	239	-
Апрель-июнь	201	-
		229,75
Июль-сентябрь	182		240,375	-58,375
		251
Октябрь-декабрь	297		260,625	+36,375
		270,25
Январь-март 19х7	324		279,625	+44,375
		289
Апрель-июнь	278		299,875	-21,875
		310,75
Июль-сентябрь	257		320,375	-63,375
		330
Октябрь-декабрь	384		340,25	+43,75
		350,5
Январь-март 19х8	401		360,25	+40,75
		370
Апрель-июнь	360		379,75	-19,75
		389,5
Июль-сентябрь	335		399,5	-64,5
		409,5
Октябрь-декабрь	462	-
Январь-март 19х9	481	-

Все эти расчеты могут быть выполнены с использованием Надстройки Пакет анализа в EXCEL (см. пример 1):

• В меню Сервис выберите команду Сервис – Анализ данных.

• Появится диалоговое окно Анализ данных. Из списка выберите инструмент анализа Скользящее среднее и щелкните на кнопке ОК.

• Появится диалоговое окно Скользящее среднее.

• В поле Входной интервал наберите данные о вашей базовой линии либо укажите диапазон в рабочем листе, ссылка на него появится в этом поле.

• В поле Интервал введите количество месяцев, которые хотите включить в подсчет скользящего среднего (для 4-звенной скользящей средней – четыре).

• В поле ввода Выходной интервал введите адрес ячейки, с которой хотите начать вывод результата (либо просто щелкните на этой ячейке в рабочем листе).

• Щелкните на кнопе ОК.

EXCEL выполняет работу по вычислению скользящего среднего, значения которого начинаются с #НД из-за недостаточного количества данных для вычисления нескольких первых результатов наблюдений.

Для каждого квартала мы имеем теперь оценки сезонной компоненты, которые включают в себя ошибку, или остаток (табл. 1.6). Прежде, чем мы сможем использовать сезонную компоненту, нужно пройти два следующих этапа. Во-первых, найдем средние значения сезонных оценок для каждого сезона года. Эта процедура позволит уменьшить некоторые значения ошибок. Во-вторых, скорректируем средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы общая их сумма равнялась нулю. Это необходимо для усреднения сезонной компоненты в целом за год. Необходимые вычисления удобно выполнить в таблице (см. таблицу 1.7).

Таблица 1.7 – Расчет средних значений сезонной компоненты

	Год	Номер квартала
		1	2	3	4
	19х6 19х7 19х8	- +44,375 +40,75	- -21,875 -19,75	-58,375 -63,375 -64,5	+36,375 +43,75 -
Итого		+85,125	- 41,625	-186,25	+80,125
Оценка сезонной компоненты (средняя)		+42,56	-20,81	-62,08	+40,06	Сумма -0,27
Скорректированная сезонная компонента		+42,6	-20,7	-62,0	+40,1	Сумма 0

Значения сезонной компоненты еще раз подтверждают наши выводы, сделанные на основе анализа диаграммы: объемы продаж за два зимних квартала превышают среднее трендовое значение примерно на 40 тыс. шт., а объемы продаж за два летних периода ниже средних на 21 и 62 тыс. шт. соответственно.

Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Если, например, в качестве сезонов выступают дни недели, то для исключения влияния ежедневной «сезонной компоненты» также рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, т.е. в четверг; таким образом, необходимость в процедуре центрирования отпадает.

Этап 2. Десезонализация данных при расчете тренда заключается в вы-

читании соответствующих значений сезонной компоненты из фактических данных за каждый квартал, т.е. У – С = Т + Е (см. табл. 1.8, столбцы 2 – 4).

Новые оценки значений тренда, которые еще содержат ошибку, можно использовать для построения модели основного тренда. Если нанести эти значения на исходный график, то можно сделать вывод о наличии линейного тренда.

Таблица 1.8 - Расчет десезонализированных данных и ошибок

Номер квартала	Объем продаж, тыс.шт. У	Сезонная компонента S	Десезонализированный объем продаж, тыс.шт. У – S = Т+Е	Трендовое значение, тыс.шт. Т	Ошибка, тыс.шт. У – S –Т=Е
1	2	3	4	5	6
1 2 3 4 5 6 7 8 9 10 11 12 13	239 201 182 297 324 278 257 384 401 360 335 462 481	(+42,6) (-20,7) (-62,0) (+40,1) (+42,6) (-20,7) (-62,0) (+40,1) (+42,6) (-20,7) (-62,0) (+40,1) (+42,6)	196,4 221,7 244,0 256,9 281,4 298,7 319,0 343,9 358,4 380,7 397,0 421,9 438,4	200 220 240 260 280 300 320 340 360 380 400 420 440	-3,6 +1,7 +4 -3,1 +1,4 -1,3 -1,0 +3,9 -1,6 +0,7 -3,0 +1,9 -1,6

Итак, уравнение линии тренда представим в виде:

Т = a + b t, (1.22)

где a и b характеризуют точку пересечения с осью ординат и наклон лини тренда соответственно, а t – номер квартала. Для определения параметров прямой, наилучшим образом аппроксимирующей тренд, можно использовать метод наименьших квадратов, в соответствии с которым величины оценок a и b определяются следующим образом:

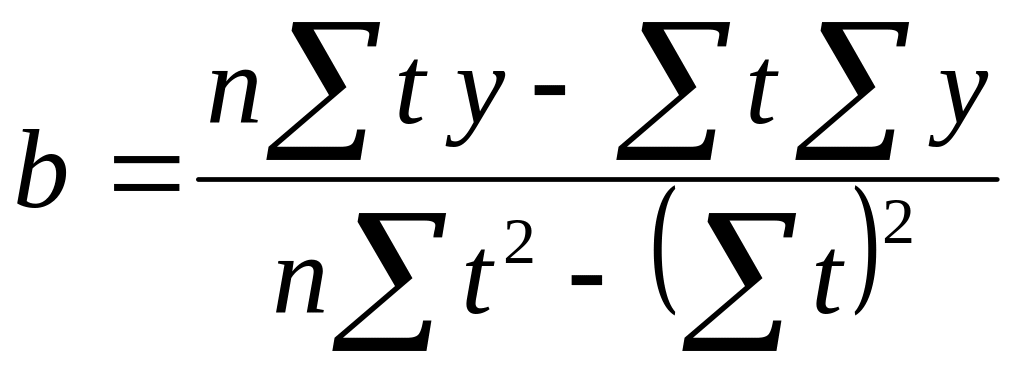, , (1.23)

где - количество наблюдений (длина временного ряда),

- значение (Т + Е ) в 4-м столбце табл. 1.8.

С помощью калькулятора можно подсчитать: t = 91, t² = 819, yt = 32746,2, y = 4158,6, n = 13.

Подставив найденные значения в соответствующие формулы (1.23), получим: b = 19,978, a = 180,046.

Следовательно, уравнение тренда (с учетом округления) имеет вид:

Т = 180 +20 t.

Построение модели тренда можно выполнить средствами EXCEL: в случае линейного тренда – посредством функции ЛИНЕЙН; нелинейного – ЛГРФПРИБЛ или, после приведения уравнения к линейному виду, функции ЛИНЕЙН; кроме того, поскольку тренд описывает изменение исследуемого показателя во времени, т.е. имеет место парная регрессия, то параметры модели можно определить с помощью мастера диаграмм.

Этап 3, предшествующий составлению прогнозов, состоит в исследовании ошибок тренда, или остатков (см. столбец 6 табл. 1.8) т.е. в подтверждении адекватности трендовой модели.

Проверим случайность остаточной последовательности, используя критерий серий.

В следующей таблице представлен исходный ряд остатков и вариационный ряд (по возрастанию уровней ряда остатков). Видим, что медиана е_м = -1. В столбце 2 знаки «+» и «-» характеризуют разность уровней исходного ряда и медианы и образуют «серии». Количество серий равно 11, а длина максимальной составляет 2.

Исходный ряд остатков (Еt)		Вариационный ряд
1	2	3
-3,6	-	-3,6
1,7	+	-3,1
4	+	-3
-3,1	-	-1,6
1,4	+	-1,6
-1,3	-	-1,3
-1		-1
3,9	+	0,7
-1,6	-	1,4
0,7	+	1,7
-3	-	1,9
1,9	+	3,9
-1,6	-	4

Сравнивая фактические значения K_max и V с критическими, видим, что условия случайности ряда остатков в соответствии с критерием серий выполнены:

K_max = 2 < [3,3 ( lg + 1)] = [3,3 (lg 13 + 1)] = [ 6,976] = 6,

V = 11 > [ ( +1 – 1,96 )] = [ ( 13 +1 – 1,96 )] = [3,605] = 3.

Выполним проверку на нормальный закон распределения.

(Еt)2	(Еt)3	(Еt)4
12,96	-46,656	167,9616
2,89	4,913	8,3521
16	64	256
9,61	-29,791	92,3521
1,96	2,744	3,8416
1,69	-2,197	2,8561
1	-1	1
15,21	59,319	231,3441
2,56	-4,096	6,5536
0,49	0,343	0,2401
9	-27	81
3,61	6,859	13,0321
2,56	-4,096	6,5536
Суммы
79,54	23,342	871,087

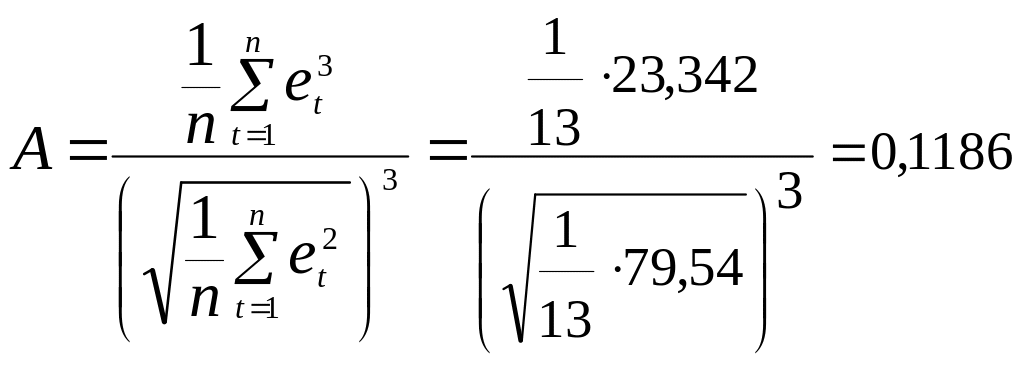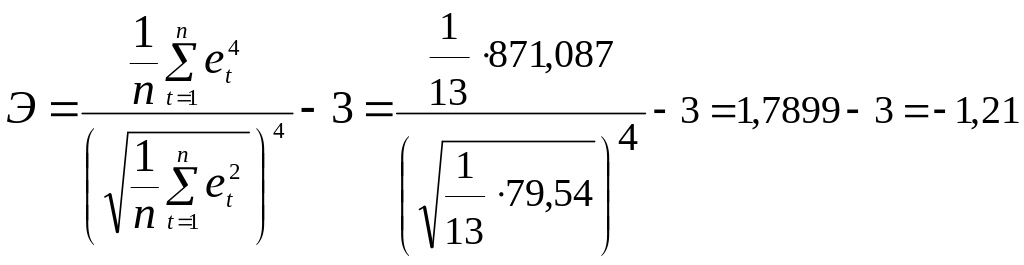, , (1.5)

, .

Итак, имеем: А= 0,1186 < 1,5 _A = 0,814;

Э +  = 0,7815 < 1,5 _Э = 1,1696.

Оба неравенства выполнены, т.е. можно с вероятностью 0,95 считать наличие нормального закона распределения случайных уровней ряда остатков установленным.

Проверим гипотезу о равенстве нулю математического ожидания остатков:

= < t_табл,

т.е. и это свойство остаточной последовательности выполнено.

Наконец, по критерию Дарбина-Уотсона выполним проверку остатков на независимость.

Et	Et-Et-1	(Et-Et-1)2
-3,6
1,7	5,3	28,09
4	2,3	5,29
-3,1	-7,1	50,41
1,4	4,5	20,25
-1,3	-2,7	7,29
-1	0,3	0,09
3,9	4,9	24,01
-1,6	-5,5	30,25
0,7	2,3	5,29
-3	-3,7	13,69
1,9	4,9	24,01
-1,6	-3,5	12,25
	Сумма=220,92

,

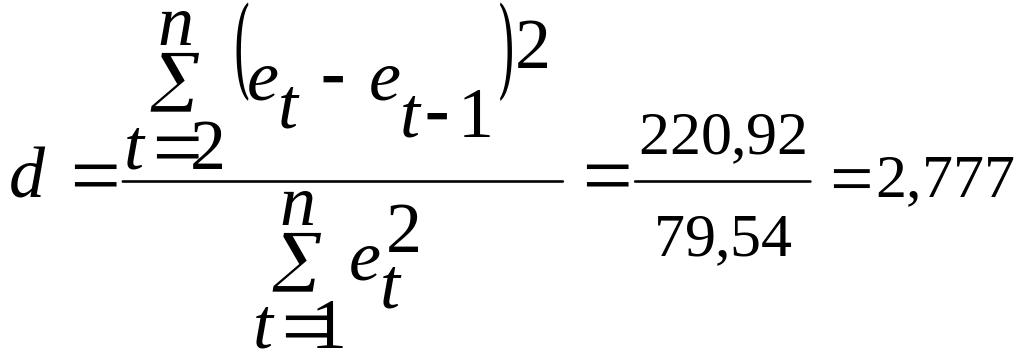d’ = 4 – d = 1,223.

Табличные значения d-статистики для n = 13: d_H = 1,01 d_В = 1,34.

Вычисленное значение d-статистики находится между d_H и d_В , поэтому гипотеза о независимости уровней ряда остатков может считаться выполненной условно (нужны дополнительные исследования).

Таким образом, по результатам проверки всех свойств ряда остатков модели можно сделать вывод о ее соответствии (адекватности) исследуемому процессу и возможности ее использования для анализа и прогнозирования.

Для определения точности модели можно использовать показатели среднего абсолютного отклонения (MAD) и среднеквадратической ошибки (MSE):

,

Как видим, ошибки достаточно малы (составляют от 1 до 2 % по отношению к исходным данным), т.е. выявленная тенденция достаточно устойчива и позволяет получить хорошие краткосрочные прогнозы.

Этап 4. Прогнозные значения по модели с аддитивной компонентой рассчитываются следующим образом:

F = T + C (тыс. шт. за квартал).

Порядковый номер квартала, включающего ближайшие три месяца с апреля по июль 19х9 г. равен 14, таким образом, прогнозное трендовое значение составит: Т₁₄ = 180 + 2014 = 460 (тыс. шт. за квартал).

Соответствующая сезонная компонента равна - 20,7 тыс. шт. (2-й квартал года). Следовательно, прогноз на этот квартал:

F_{(апрель - июнь 19х9 г.)} = 4600 – 20,7 = 439,3 тыс. шт.

Не следует забывать, что чем длиннее период упреждения, тем меньшей оказывается обоснованность прогноза.

В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения. Таким образом, значения сезонной компоненты увеличиваются с возрастанием значений тренда.

Пример.

Компания осуществляет реализацию нескольких видов продукции. Объем продаж одного из них за последние 13 кварталов представлены в таблице 3.15.

Таблица 3.15 Квартальные объемы продаж компании

Дата	Номер квартала	Количество проданной продукции, тыс. шт.
Январь – март 19х6	1	70
Апрель – июнь	2	66
Июль – сентябрь	3	65
Октябрь - декабрь	4	71
Январь – март 19х7	5	79
Апрель – июнь	6	66
Июль – сентябрь	7	67
Октябрь - декабрь	8	82
Январь – март 19х8	9	84
Апрель – июнь	10	69
Июль – сентябрь	11	72
Октябрь - декабрь	12	87
Январь – март 19х9	13	94

Построим по этим данным точечную диаграмму (рис. 4).

Рисунок 4. - Квартальные объемы продаж компании

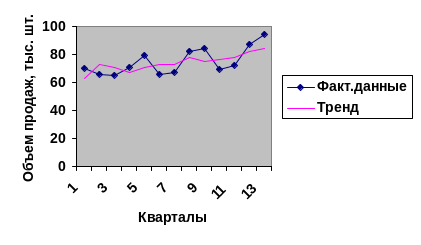
Объем продаж этого продукта (так же, как и в предыдущем примере) подвержен сезонным колебаниям, и значения его в зимний период выше, чем в летний. Однако, размах вариации фактических значений относительно линии тренда постоянно возрастает. К таким данным следует применять модель с мультипликативной компонентой:

Фактическое значение = Трендовое значение х Сезонная вариация х Ошибка,

т.е.

А = Т*С*Е. (3.23)

В нашем примере есть все основания предположить существование линейного тренда, но чтобы полностью убедиться в этом, проведем процедуру сглаживания временного ряда. Эта процедура ничем не отличается от той, которая применялась для аддитивной модели, кроме того, что теперь оценки сезонной компоненты следует определять по формуле

А / Т = С * Е. (3.24)

Результаты расчетов приведены в табл. 3.16, причем для вычисления скользящих средних использован Пакет анализа в EXCEL (см. пример 2).

Таблица 3.16 Расчет значений сезонной компоненты

Номер квартала	Объем продаж, тыс. шт. (А)	Скользящая средняя за 4 квартала	Центрированная скользящая средняя (Т)	Коэффициент сезонности А / Т = С*Е
1	2	3	4	5
1	70
2	66
		68
3	65		69,125	0,940
		70,25
4	71		70,25	1,011
		70,25
5	79		70,50	1,121
		70,75
6	66		72,125	0,915
		73,50
7	67		74,125	0,904
		74,75

Продолжение таблицы 3.16

1	2	3	4	5
8	82		75,125	1,092
		75,50
9	84		76,125	1,103
		76,75
10	69		77,375	0,892
		78
11	72		79,25	0,909
		80,50
12	87		-	-
13	94		-	-

Так как значения сезонной компоненты в данном случае – это доли, а число сезонов равно 4, то сумма компонент должна равняться 4 (количеству сезонов), а не нулю, как в предыдущем случае. Если эта сумма не равна 4, то производится корректировка значений сезонной компоненты точно таким же образом, как это уже делалось ранее. Корректировка выполнена в таблице 3.17.

Таблица 3.17 Расчет сезонной компоненты

	Год	Номер квартала
		1	2	3	4
	19х6	-	-	0,940	1,011
	19х7	1,121	0,915	0,904	1,092
	19х8	1,103	0,892	0,909	-
Итого		2,224	1,807	2,753	2,103
Средние Значения		2,224 / 2	1,807 / 2	2,753 / 3	2,103 / 2
Оценка сезонной компоненты		1,112	0,903	0,918	1,051	Сумма = = 3,984
Скорректи- рованная сезонная компонента3		1,116	0,907	0,922	1,055	Сумма = = 4

Как показывают оценки, в результате сезонных воздействий объемы продаж в январе – марте увеличиваются на 11,6% соответствующего значения тренда (1,116). Аналогичные сезонные воздействия в октябре – декабре приводят к увеличению объема продаж на 5,5% от соответствующего значения тренда. В двух других кварталах сезонные воздействия состоят в снижении объемов продаж, которое составляет 90,7 и 92,2% от соответствующих трендовых значений.

После определения оценок сезонной компоненты приступим к процедуре десезонализации данных по формуле:

А / С = Т * Е. (3.25)

Результаты расчетов этих оценок приведены в таблице 3.18.

Таблица 3.18 Расчет уравнения тренда для компании

Дата	Номер квартала	Объем продаж, тыс. шт. А	Коэффициент сезонности С	Десезонализирован-ный объем продаж, тыс. шт. А / С = Т * Е
Январь-март 19х6	1	70	1,116	62,7
Апрель-июнь	2	66	0,907	72,8
Июль-сентябрь	3	65	0,922	70,5
Октябрь-декабрь	4	71	1,055	67,3
Январь-март 19х6	5	79	1,116	70,8
Апрель-июнь	6	66	0,907	72,8
Июль-сентябрь	7	67	0,922	72,7
Октябрь-декабрь	8	82	1,055	77,7
Январь-март 19х6	9	84	1,116	75,3
Апрель-июнь	10	69	0,907	76,1
Июль-сентябрь	11	72	0,922	78,1
Октябрь-декабрь	12	87	1,055	82,5
Январь-март 19х6	13	94	1,116	84,2

Полученные трендовые значения нанесем на исходную диаграмму (рис. 4). Очевидно, что линия тренда – не кривая, наоборот, она несколько больше напоминает прямую, хотя отдельные точки, особенно значения за 19х6 г., расположены хаотично. Предположим для простоты, что тренд линейный, и для расчета параметров прямой, наилучшим образом его аппроксимирующей, применим метод наименьших квадратов. Воспользуемся той же процедурой, что и в примере 2:

Таблица 3.19 Рабочий лист EXCEL

Расчет параметров уравнения тренда												Трендо вые		Расчет ошибок
Исходные данные										значе- ния
А	t	С		Вывод результатов						Т			Т*С			Е=А/Т* С		Е=А –Т*С
1	2	3		4				5			6				7		8
70	1	1,116		1,63186		63,3461		64,9780			72,51547				0,96531		-2,5154
66	2	0,907		0,53715		4,26351		66,6098			60,41517				1,09244		5,5848
65	3	0,922		0,45623		7,24658		68,2417			62,91890				1,03307		2,0810
71	4	1,055		9,22942		11		69,8736			73,71667				0,96314		-2,7166
79	5			484,664		577,642		71,5054			79,80013				0,98997		-0,8001
66	6							73,1373			66,33558				0,99494		-0,3355
67	7			Т=63,35+1,63 t						74,7692			68,93723			0,97189		-1,9372
82	8							76,4011			80,60315				1,01733		1,3968
84	9							78,0329			87,08479				0,96457		-3,0847
69	10							79,6648			72,25600				0,95493		-3,2560
72	11							81,2967			74,95556				0,96056		-2,9555
87	12							82,9285			87,48964				0,99440		-0,4896
94	13							84,5604			94,36945				0,99608		-0,3694

Таким образом, уравнение тренда выглядит следующим образом:

Т = 63,35 + 1,63 * номер квартала (тыс. шт. в квартале).

Это уравнение можно использовать в дальнейшем для расчета оценок трендовых объемов продаж на каждый момент времени (см. табл. 3.20). Кроме того, трендовые значения можно определить с помощью функции ТЕНДЕНЦИЯ в EXCEL, как это сделано в табл. 3.19, гр. 5 ⁴.

После нахождения тренда и сезонной компоненты можно рассчитать ошибки в прогнозируемых по модели объемах продаж (Т*С) по сравнению с фактическими значениями (А). В табл. 3.20 эти ошибки рассчитаны как отношение Е = А / (Т*С).

Таблица 3.20 Расчет трендовых значений и ошибок Е₁ и Е₂

Номер квартала t	Объем продаж, тыс. шт. А	Сезонная компо- нента С	Трендовое значение, тыс. шт. Т=63,35+1,63t	Ошибка
				Т * С	Е1 = = А/ Т*С	Е2 = А- -(Т*С)
1	70	1,116	65,0	72,51	0,96	-2,5
2	66	0,907	66,6	60,41	1,09	+5,6
3	65	0,922	68,2	62,92	1,03	+2,1
4	71	1,055	69,9	73,72	0,96	-2,7
5	79	1,116	71,5	79,80	0,99	-0,8
6	66	0,907	73,1	66,34	0,99	-0,3
7	67	0,922	74,8	68,94	0,97	-1,9
8	82	1,055	76,4	80,60	1,02	+1,4
9	84	1,116	78,0	87,08	0,96	-3,1
10	69	0,907	79,7	72,26	0,95	-3,3
11	72	0,922	81,3	74,96	0,96	-3,0
12	87	1,055	82,9	87,49	0,99	-0,5
13	94	1,116	84,6	94,37	1,00	-0,4

Вычисленные по е₁ и е₂ средняя абсолютная и среднеквадратическая ошибки имеют следующие значения соответственно:

1. MAD = 12,9 / 13 = 0,99; MSE = 12,82 / 13 = 0,986;

2. MAD = 27,5 / 13 = 2,12; MSE = 84,915 / 13 = 6,53.

После того, как параметры уравнения тренда определены, процедура составления прогнозов становится очевидной. Прогнозные значения определяются по формуле:

F = Т * C, (3.26)

где

Т = 63,35 + 1,63 * номер квартала (тыс. шт. за квартал),

а сезонные компоненты составляют 1,116 в первом квартале, 1,097 – во втором,

0,922 – в третьем и 1,055 в четвертом квартале. Ближайший следующий квартал – это второй квартал 19х9 г., охватывающий период с апреля по июнь и имеющий во временном ряду порядковый номер 14. Прогноз объема продаж в этом квартале составляет:

F = Т*C = (63,35 + 1,63 *14)*0,907 = 86,17 * 0,907 = 78,2 (тыс. шт. за квартал).

Аналогично, прогноз на октябрь – декабрь 19х9 г. рассчитывается для квартала с порядковым номером 16 с использованием значения сезонной компоненты для 4-го квартала года:

F = Т*C = (63,35 + 1,63 *16)*1,055 = 89,43 * 1,055 = 94,3 (тыс. шт. за квартал).

Разумно предположить, что величина ошибки данного прогноза будет несколько выше, чем предыдущего, поскольку этот прогноз рассчитан на более длительную перспективу.