§6. Класіфікацыя рухаў плоскасці. Групы рухаў.

Пункт з’яўляецца інварыянтным пры руху f толькі тады, калі M’(x’, y’)=f(M)=M(x, y), г. зн. калі

_{ x'  x}

_

 ^{y'  y}

_{З аналітычных выразаў руху будзе}

_ x(1  cos )  y sin  x₀

_

_^{ x sin  (1   cos ) y  y}₀

Адносна x і y гэта есць лінейная сістэма двух раўнанняў. Даследуем яе па формулах Крамера.

Асноўны вызначальнік сістэмы

_{1  cos}

_{ }

 sin 

 sin 

_{1   cos}

 1  cos   cos   cos²    sin ²  

_{ (1  cos )(1   )  2(1   ) sin} ^{2 }

²

Разгледзім спачатку класіфікацыю рухаў першага роду, г. зн. калі  =1. Магчымы выпадкі:

_{1)   0    0  i'  i}

Сістэма раўнанняў (1) мае адзінае рашэнне x= x₁ ,

y  y₁

. Рух мае адзін інварыянтны

пункт

M₁ (x₁ , y₁ ) . Легка ўпэўніцца, што рух з’яўляецца паваротам плоскасці вакол пункта

^M ₁ ^{на вугал  .}

_{2)   0    0; i'  i, j'  j}

З аналітычных выразаў руху атрымаем

_ x'  x  x₀

_

 ^{y' y  y}0

Значыць, рух з’яўляецца паралельным пераносам.

Аналагічна можна даказаць, што рухі другога роду могуць быць толькі восевай сіметрыяй, ці слізготнай сіметрыяй.

_{Абазначым праз P- мноства ўсіх рухаў плоскасці. На падставе азначэння руху маем f, g}

 P  g  f  P і

f  P  f ^1  P

. Такім чынам, P- гэта падгрупа групы G усіх

пераўтварэнняў плоскасці. Яна называецца групай рухаў. Асноўным яе інварыянтам з’яўляецца адлегласць паміж пунктамі.

₁₅ ^{Відавочна, што мноства P}_

yсіх рухаў першага роду есць падгрупа групы P усіх рухаў.

Яе асноўны інварыянт- гэта арыентацыя вугла.

Мноства ўсіх паралельных пераносаў з’яўляецца падгрупай групы рухаў.Напрамак есць

_{яе асноўны інварыянт.}

Падгрупай групы

^_ ^{, а таму і групы  , з’яўляецца і мноства ўсіх паваротаў плоскасці}

вакол пункта

^М ₀ ^{. Асноўны інварыянт – гэта адлегласць ад цэнтра павароту}

^М ₀ ^.

Мноства рухаў другога роду групу не ўтварае.

§ 7. Гаматэтыя і яе ўласцівасці.

_{Няхай дадзены пункт S і сапраўдны лік k≠0. Разгледзім адлюстраванне плоскасці на}

_{сябе па закону}

_{SM '  k  SM , дзе M’ – гэта вобраз пункта M. Яно з’яўляецца}

пераўтварэннем плоскасці і называецца гаматэтыяй. Пункт S называецца цэнтрам, а лік k –

каэфіцыентам гаматэтыі. Калі k>0 , то гаматэтыя называецца дадатнай, а пры k<0 –

H

_{адмоўнай. Абазначым гаматэтыю} ^k _{. Калі k=1, то маем тоеснае пераўтварэнне. Цэнтр S}

^s

гаматэтыі есць інварыянтны пункт і пры

k>0.

k  1

іншых інварыянтных пунктаў няма. Няхай

_{K K}

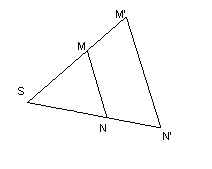
^{N '  H} _S ^{( N ) , M '  H} _S ^{(M ) }

_{M ' N '  SN '  SM ', M ' N '  k  MN}

SN '  k  SN , SM '  k  SM ;

Аналаічна і для k<0.

Такім чынам, гаматэтыя ўсялякі вектар MN памнажае на каэфіцыент гаматэтыі k. Карыстаючыся гэтым, можна пераканацца, што гаматэтыя захоўвае стасунак, у якім

пункт дзеліць накіраваны адрэзак. Таму гаматэтыя пераводзіць адрэзак у адрэзак, прамень

у прамень, прамую ў прамую, паўплоскасць у паўплоскасць, вугал у вугал. Кожная прамая, якая праходзіць праз цэнтр гаматэтыі, інварыянтна. Дадатная гаматэтыя захоўвае любы напрамак, а адмоўная змяняе яго на процілеглы.

H

_{Няхай дадзеная адмоўная гаматэтыя} ^k _{пераводзіць пункт M у M’. Тады}

^s

_k

SM '   k  SM

. Калі

H _S ^{(M )  M " , то}

^{SM "  k  SM} . Адсюль маем

SM '  SM " .

Значыць, пункты M’ і M” сіметрычныя адносна цэнтра S гаматэтыі, прычым для любога

_k

пункта M плоскасці

^{M ' } Z _S ^{( M " )}

^{, M ' } Z _S ^ H _S ^{(M )}

для

M . Значыць,

_{k k}

^H _S ^{ Z} _S ^{ H} _S ^.

_k

^{Такім чынам, адмоўная гаматэтыя H} _s ^{з’яўляецца кампазіцыяй дадатнай гаматэтыі з}

^{тым жа цэнтрам S і каэфіцыентам k і цэнтральнай сіметрыі} _{Z S} ^{адносна пункта S.}