5.Законы Ньютона и примеры проявления

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Пример. В качестве примера выполнения 1 закона Ньютона можно рассмотреть движение парашютиста (см. рис. 2). Он равномерно приближается к земле, когда действие силы тяжести компенсируется силой натяжения строп парашюта, которая в свою очередь обусловлена сопротивлением воздуха.

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Пример. На рис. 3 показано, как движется мяч после столкновения с битой. Чем больше сила удара, тем   с большим ускорением начнет двигаться мяч и, следовательно, тем большую скорость он приобретет за время удара.

 

Третий закон Ньютона  Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой  , а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Пример. На рис. 5 показано взаимодействие космонавта и спутника (космонавт пытается придвинуть спутник к себе). Они действуют друг на друга с равными по величине, но противоположными по направлению силами. Отметим, что ускорения, с которыми космонавт и спутник будут перемещаться в космическом пространстве будут разными из-за разницы в массах этих объектов.

Законы Ньютона позволяют объяснить закономерности движения планет, их естественных и искусственных спутников. Иначе, позволяют предсказывать траектории движения планет, рассчитывать траектории космических кораблей и их координаты в любые заданные моменты времени. В земных условиях они позволяют объяснить течение воды, движение многочисленных и разнообразных транспортных средств (движение автомобилей, кораблей, самолетов, ракет). Для всех этих движений, тел и сил справедливы законы Ньютона.

6.Закон сохранение импульса.Центр масс

1) Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

2) Центр масс (центр ине́рции; барице́нтр) в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

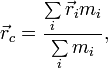
где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибовес массы P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.