3. Теплопередача через плоскую стенку

Для получения расчетной формулы теплового потока при тепло­передаче рассмотрим теплопроводность многослойной плоской стен­ки при граничных условиях третьего рода. Стенка состоит из п слоев с известными толщинами и коэффициентами теплопроводности (рис. 3.5). Известны также контактные термические сопротивления между отдельными слоями. Теплоносители имеют температуры и , а интенсивность их теплообмена с поверхностями стенки определяется коэффициентами и .

П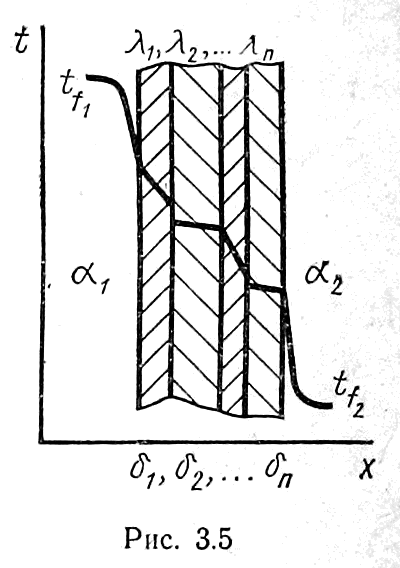 ри стационарном режиме теплообме­на плотности теплового потока от пер­вого теплоносителя к стенке, через стен­ку и от стенки ко второму теплоноси­телю одинаковы. С учетом формул (1.19) и (3.10) для многослойной плоской стен­ки плотности теплового потока опреде­ляются выражениями:

Выразив из этих уравнений разности температур в явном виде и просуммировав, левые и правые части полученных равенств, найдем формулу для плотности теплового потока:

где к — коэффициент теплопередачи, который выражается равенством

Величина, обратная коэффициенту теплопередачи , называется общим термическим сопротивлением

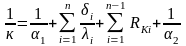
Из формулы (3.17) видно, что общее термическое сопротивление складывается из внешних термических сопротивлений ( и ), внутренних термических сопротивлений отдельных слоев ( ) и контактных термических сопротивлении между ними ( ),

Температуры крайних поверхностей стенки определяются из равенств (3.12) и (3.14):

; .

Температуры на поверхностях отдельных слоев стенки рассчиты­ваются по формулам теплопроводности. Температурное поле при теплопередаче через плоскую стенку показано на рис. 3.5.

§4. Теплопроводность цилиндрической стенки

Рассмотрим теплопроводность однородной цилиндрической стенки большой длины так, чтобы передачей теплоты с торцом трубы можно было пренебречь (рис. 3.6). Если внутренняя и внешняя поверхности поддерживаются при постоянных температурах t_w1 и t_w2, то тепловой поток имеет радиальное направление, а изотермические поверхности имеют форму цилиндров. В этих условиях температурное поле t=f(r) будет одномерным.

Размеры стенки оценим радиусами r₁, r₂ и длиной l, а коэффициент теплопроводности будем считать одинаковым для всей стенки.

Для стационарной одномерной задачи о теплопроводности цилиндрической стенки без внутренних источников теплоты дифференциальное уравнение энергии (2.15) с учетом (2.16) приводится к виду

(3.18)

Введение новой переменной

(3.19)

позволяет привести уравнение (3.18) к виду

(3.20)

После разделения переменных и интегрирования получим

(3.21)

Потенцирование этого выражения, переход к первоначальным переменным и интегрирование дает

(3.22)

С ледовательно, зависимость t=f(r) носит логарифмический характер (рис. 3.6).

Искривление линии температурного поля в цилиндрической стенке обусловлено изменением плотности теплового потока при изменении радиуса цилиндра: при уменьшении радиуса площадь поверхности, через которую проходит тепло, также уменьшается. Поэтому на малых радиусах температурная линия проходит более круто. Это правило остается в силе и при обратном направлении теплового потока (пунктир на рис. 3.6).

Граничные условия первого рода записываются равенствами:

при

при

Подставив эти выражения в равенство (3.22), получим:

(3.23)

Заменив в уравнении (3.22) константы интегрирования выражениями (3.23), получим формулу температурного поля

(3.24)

где и - внутренний и наружный диаметры цилиндра; d – переменный диаметр.

Тепловой поток через изотермическую поверхность с радиусом r можно оценить по закону Фурье:

(3.25)

Из формулы (3.24) получается следующее выражение для температурного градиента:

(3.26)

После подстановки выражения (3.26) в (3.25) найдем

(3.27)

Если отнести тепловой поток к единице длины цилиндрической стенки, то формула (3.27) перепишется в виде

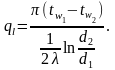(3.28)

Величину называют внутренним термическим сопротивлением цилиндрической стенки.

Обозначим плотности теплового потока на внутренней и внешней поверхностях через q₁ и q₂. Так как

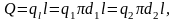
то

Это выражение можно использовать для подсчета q₁ или q₂ по величине q_l.

Если <2, т.е. труба тонкостенная, то кривизна стенки слабо влияет на величину теплового потока. В этом случае (с точностью до 4%) для определения теплового потока вместо выражения (3.28) можно использовать формулу плоской стенки

(3.29)

где d_ср – средний диаметр цилиндрической стенки.

Выведем формулу для определения теплового потока через мно­гослойную цилиндрическую стенку, состоящую из п слоев (рис. 3.7), с учетом контактного термического сопротивления. Тепловой поток через поверхность контакта с диаметром d выразится формулой

(3.30)

При стационарном режиме величины q_l одинаковы для всех участков теплового тракта. Их можно определить с помощью фор­мул (3.28) и (3.30):

(3.31)

Выразив из этих равенств в явном виде разности температур и просуммировав левые и правые части равенств, после перестановки членов найдем

(3.32)

Если контактными термическими сопротивлениями можно пре­небречь, то в формуле (3.32)

Температуры на поверхностях отдельных слоев определяются по формулам, которые выводятся так же, как для плоской стенки. Так, для оценки температуры формула имеет вид

(3.33)

Температурное поле многослойной цилиндрической стенки по­казано на рис. 3.7.