Формула Тейлора для основных элементарных функций.

Общий вид формулы Тейлора для функций:

, где - остаточный член.

При получаем так называемую формулу Маклорена.

Формула Тейлора для важнейших элементарных функций:

1) ,

, , . Отсюда получаем, что

. ,

, где . И в итоге имеем: , , .

Пример:

Пусть , тогда получим:

, .

2) ,

Поскольку , , формула имеет вид: , где n – нечётное число, а остаточный член в форме Лагранжа равен , .

Очевидно, что для остаточного члена справедлива следующая оценка: .

3) ,

Поскольку , то

, ,

, , .

4) ,

, , , ,

,

, при ,

Рассмотрим остаточный член в форме Коши:

, , ,

, где , и .

5) ,

, , ,

,

Остаточный член в форме Пеано.

Билет 22 Выпуклость функции в точке. Достаточное условие.

Определение: Функция f(x) называется выпуклой вверх (вниз) в точке x_o, если найдется такая окрестность U(x_o), что для всех точек из этой окрестности U(x_o) график функции f(x) лежит не выше (не ниже) касательной, проведенной в точке x_o.

З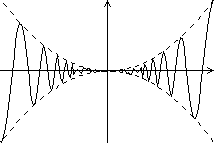 амечание: Говорить о выпуклости в точке можно только если функция дифференцируема в этой точке.

Контрольный пример: . 0 - ни точка выпуклости вверх, ни точка выпуклости вниз, ни точка перегиба, потому что в любой окрестности U(0) есть точки в которых функция выпукла вверх и вниз.

Теорема: (Достаточное условие выпуклости вверх (вниз)).

Если функция f в точке x_o имеет непрерывную вторую производную , и при этом <0 (>0), то f выпукла в вверх (вниз) в точке x_o.

Доказательство:

Т.к. функция f имеет непрерывную вторую производную , то эта производная определена в некоторой окрестности . Разложим функцию f по формуле Тéйлора с остаточным членом в форме Пеано:

.

Причем функция является графиком касательной к функции f в точке . Поэтому если >0, то f(x)< (x) в окрестности (т.к. ε(x)→0, при x→0), а если >0, то f(x)> (x) в .

Билет 23

Точка перегиба. Достаточные условия. Общая теорема о точках перегиба и экстремума.

Определение.

Точка называется точкой перегиба, если в этой точке график переходит через сторону касательной ( разные выпуклости слева и справа).

Замечание.

Точка перегиба существует только если . Пример

Теорема 1 (Достаточное условие существования точки перегиба).

Если функция имеет непрерывной в точке , =0 и , то точка перегиба.

Доказательство:

В этом случае: , (формула Тейлора) , или .

В силу непрерывности в и того факта, что сохраняет знак в некоторой окрестности точки . С другой стороны, множитель меняет знак при переходе через , а вместе с ним и величина (равная превышению точки кривой над касательной в ) меняет знак при переходе через .

Теорема доказана.

Теорема 2 (Общая теорема о точках перегиба и экстремума.)

Пусть функция обладает следующими свойствами:

Непрерывна в и . Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или , а если четное, то есть точка перегиба кривой.

Доказательство:

Разложим по формуле Тейлора:

того же знака, что , , , если - четное, то

или всегда, - не точка перегиба.

Если - нечетная

С одной стороны , с другой стороны - точка перегиба. - четное.

, - min

, - max

Билет 24