
- •Модуль непрерывности. Равномерная непрерывность функции на множестве.
- •Равномерная непрерывность функции, непрерывной на отрезке
- •Производная. Определение, непрерывность функции, имеющей производную. Геометрический смысл производной.
- •Геометрический смысл производной.
- •Билет 4 Дифференциал функции. Определение. Геометрический смысл.
- •Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Арифметические свойства производной.
- •Производная сложной функции. Дифференциал сложной функции. Инвариантность формы первого дифференциала.
- •Производная обратной функции. Производные элементарных функций.
- •Возрастание (убывание) функции в точке. Необходимое условие, достаточное условие возрастания (убывания) функции в точке. Теорема Ферма.
- •Теорема Ролля. Геометрический и физический смысл.
- •Теорема Коши. Физический смысл.
- •Теорема Лагранжа. Геометрический и физический смысл. Формула конечных приращений.
- •Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
- •Условие постоянства функции на отрезке.
- •Достаточные условия экстремума.
- •Формула Тейлора для многочленов.
- •Формула Тейлора для дифференцируемых функций с остаточными членами в форме Пеано, Лагранжа, Коши. Единственность разложения.
- •Формула Тейлора для основных элементарных функций.
- •Билет 22 Выпуклость функции в точке. Достаточное условие.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Непрерывна в и . Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или , а если четное, то есть точка перегиба кривой.
- •Правило Лопиталя. Случай 0/0.
- •Раскрытие неопределенностей вида , , , , .
- •Асимптота. Виды асимптот. Уравнение наклонной асимптоты.
- •Первообрáзная. Неопределенный интеграл. Свойства.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям неопределенного интеграла.
- •Интегрирование простейших рациональных дробей
- •Теорема о разложении рациональной дроби на элементарные.
- •Интегрирование рациональных дробей.
- •Интегрирование тригонометрических выражений.
- •Первая подстановка Эйлера (Леонарда)
- •Интегрирование выражений вида .
- •Тригонометрические подстановки.
Теорема Коши. Физический смысл.
Теорема: (Коши о среднем)
Пусть функции f(x) и g(x) непрерывны на отрезке [a,b] и имеют производные на интервале (a,b), одновременно не обращающиеся в ноль. При этом g(b)-g(a)0 (что следует из условия g΄(x)0). Тогда на интервале (a,b) найдется точка ζ, для которой выполняется неравенство:
![]() ,
a<ζ
,
a<ζ
Доказательство: Вводим функцию H(x) = (f(b) - f(a)) · g(x) – (g(b) - g(a)) · f(x). Очевидно, что она непрерывна на [a,b] и имеет производную на (a,b), т.к. f(b) - f(a) и g(b) - g(a) постоянны. Кроме того, H(a)=H(b), поэтому по теореме Ролля найдется такая точка ζ из (a,b), что H΄(ζ)=0.
H΄(ζ) = (f(b)-f(a)) ·
g΄(ζ) – (g(b)-g(a)) · f΄(ζ) = 0
(f(b)-f(a))
· g΄(ζ) = (g(b)-g(a)) · f΄(ζ)![]() ,
т.к. по условию g(b)
- g(a)0
и g΄(x)0
на (a,b).
,
т.к. по условию g(b)
- g(a)0
и g΄(x)0
на (a,b).
Теорема доказана.
Физический смысл: Если f΄(x) и g΄(x) – скорости, то отношение перемещений равно отношению скоростей в какой-то момент времени.
Билет 15
Теорема Лагранжа. Геометрический и физический смысл. Формула конечных приращений.
Теорема:
Пусть
функция
непрерывна
на отрезке
![]() и имеет производную на интервале
и имеет производную на интервале
![]() .
Тогда существует на интервале
точка
.
Тогда существует на интервале
точка
![]() ,
для которой выполняется равенство
,
для которой выполняется равенство
![]() (1),
(1),
причем
![]() .
.
Доказательство:
В
теореме Коши, возьмем
![]() .
Тогда
.
Тогда
![]() ,
,![]() ,
,
![]() .
.
Из
теоремы Коши:
![]()
![]() теорема доказана.
теорема доказана.
Физический смысл:
Найдется
момент времени когда
![]() (средняя
скорость равна мгновенной)
(средняя
скорость равна мгновенной)
Г еометрический
смысл:
еометрический
смысл:
Теорема
Лагранжа утверждает, что если кривая
есть график непрерывной на
функции, имеющей производную на
,
то на этой кривой существует точка,
соответствующая некоторой абсциссе
![]() такая, что касательная к кривой в этой
точке параллельна хорде, стягивающей
концы кривой
такая, что касательная к кривой в этой
точке параллельна хорде, стягивающей
концы кривой
![]() и
и
![]() .
.
Равенство
(1) называется формулой
(Лагранжа) конечных приращений.
Промежуточное значение
удобно записывать в виде
![]() ,
где
,
где
![]() есть некоторое число, удовлетворяющее
неравенствам
есть некоторое число, удовлетворяющее
неравенствам
![]() .
Тогда формула Лагранжа примет вид
.
Тогда формула Лагранжа примет вид
![]()
![]()
Она
верна, очевидно, не только для
![]() ,
но и для
,
но и для
![]() .
.
Билет 16
Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
Определение:
Функция
называется строго возрастающей на
отрезке [a,b],
если для любых точек
![]() ,
,
![]() из [a,b],
удовлетворяющих неравенству
из [a,b],
удовлетворяющих неравенству
![]() ,
имеет место неравенство
,
имеет место неравенство![]() .
.
Определение:
Функция
называется неубывающей на [a,b],
если из того, что
![]() и
следует, что
и
следует, что
![]() .
.
Определение:
Функция
называется строго убывающей на отрезке
[a,b],
если из того, что
и
следует, что
![]() .
.
Определение:
Функция
называется невозрастающей на [a,b],
если из того, что
и
следует, что
![]() .
.
Пример:
![]()
Если
убывает на
![]() и на
и на
![]() ,
то нельзя говорить, что
убывает на
,
то нельзя говорить, что
убывает на
![]() .
.
Теорема 1: (необходимое условие возрастания (неубывания) функции в точке )
Если функция
возрастает (неубывает) в точке
и дифференцируема в
,
то
![]() .
.
Доказательство:
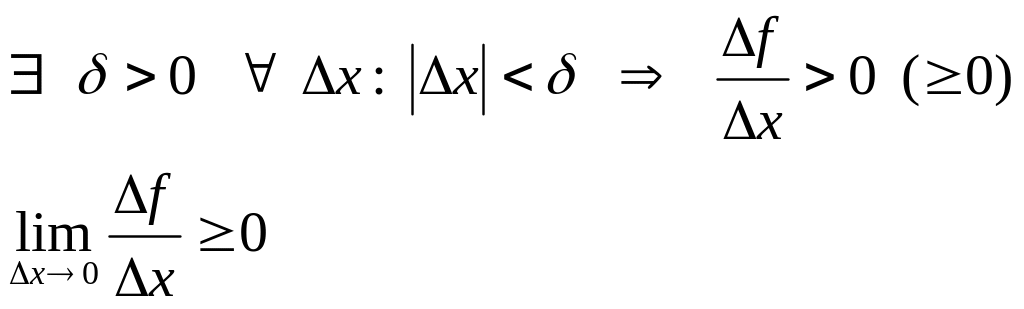
Теорема доказана.
Пример:
![]() возрастает в 0 и
возрастает в 0 и
![]()
Теорема 1’: (необходимое условие убывания (невозрастания) функции в точке )
Если функция
убывает (невозрастает) в точке
и дифференцируема в
,
то
![]() .
.
Доказательство – аналогично теореме 1.
Теорема 2: (достаточное условие возрастания)
Если функция
дифференцируема в
и
![]() ,
то
возрастает в точке
.
,
то
возрастает в точке
.
Доказательство:
![]()
![]()
![]() возрастает.
возрастает.
Теорема доказана.
Замечание: Если в точке , то ни про возрастание, ни про убывание ничего сказать нельзя.
