Производная сложной функции. Дифференциал сложной функции. Инвариантность формы первого дифференциала.
Теорема:
Пусть функция
такая, что
,
и функция
такая,
что
,
.
Тогда функция
и
.
Доказательство:
дифференцируема
в точке
,
тогда:
Рассмотрим ∆H:
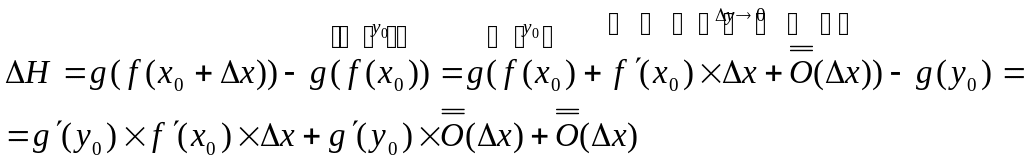
Инвариантность/Неинвариантность.
1) y(x),
x
– независимая
переменная,
,
пусть x
= x(t)
2)
y(x),
x
– независимая
переменная,
,
,
,
здесь
,
.
Билет 8
Производная обратной функции. Производные элементарных функций.
Определение:
Пусть на интервале (a,b)
задана непрерывная строго монотонная,
т.е. строго возрастающая или строго
убывающая, функция
.
Пусть образ (a,b)
есть интервал (A,B).
тогда обратная к
функция
есть однозначная непрерывная и строго
монотонная на (A,B)
функция.
Зафиксируем
и дадим ему приращение
Тогда
получит соответствующее приращение
Наоборот,
Вследствие
непрерывности прямой и обратной функций
для указанных
имеет место утверждение: из
следует
,
и обратно.
Пусть теперь
функция
в точке у имеет неравную нулю производную
.
Покажем, что в таком случае функция
также имеет в соответствующей точке х
производную. В самом деле,
Так как из того, что следует, что , то
Этим доказано, что
если
есть строго монотонная непрерывная
функция и
обратная к ней функция, имеющая в точке
у производную
,
то функция
имеет в соответствующей точке х
производную, определяемую формулой
(1).
Может случится,
что в точке
В этом случае, очевидно, функция
имеет в соответствующей точке х
производную
.
Если же
,
то для строго возрастающей функции при
этом
,
а для строго убывающей
.
В первом случае
,
а во втором
.
Пример 1.
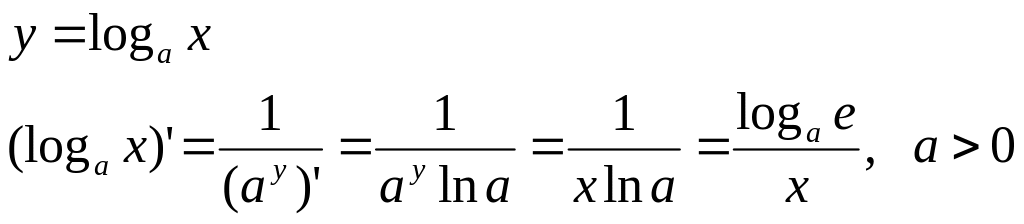
Если логарифм натуральный, то
.
Функция ln x как действительная функция определена только для положительных значений х.
Пример 2.
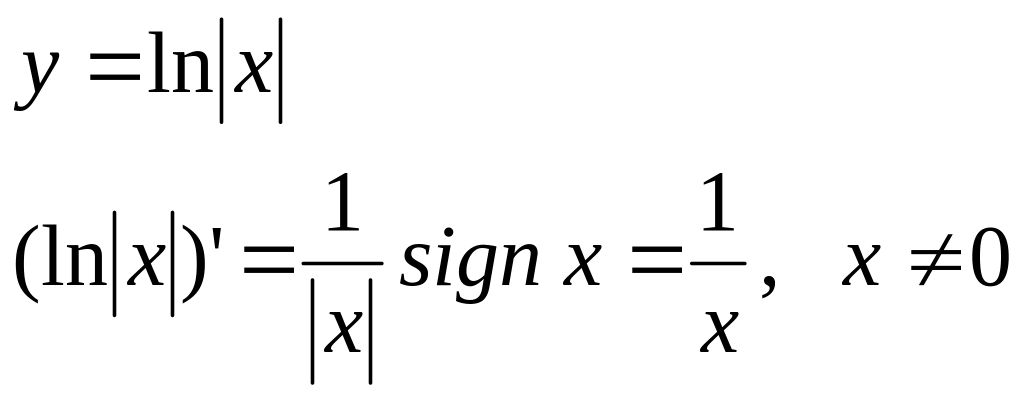
где
Пример 3.
Пример 4.
Функция
строго возрастает на отрезке [-1,1] и
отображает этот отрезок на
Обратная к ней функция
имеет производную
положительную на интервале
.
Поэтому
Пример 5.
Пример 6.
Производные элементарных функций.
1.
;
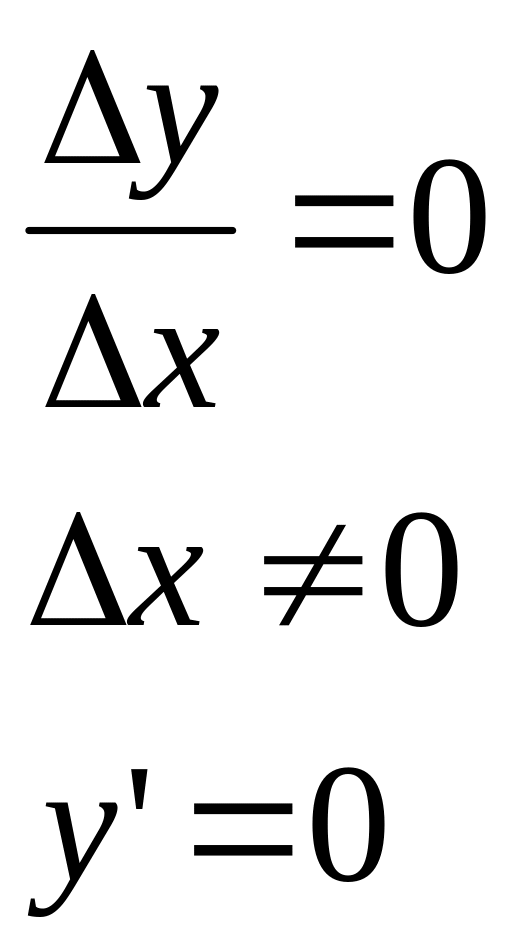
2.
3.
4.
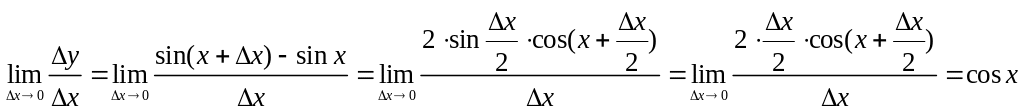(т.к. функция
непрерывна)
Замечание: если функция имеет конечную производную в точке, то она непрерывна в этой точке (было доказано в Билете 1), но она может быть разрывной в любой другой точке, кроме этой.
Билет 9
Производные высших порядков. Производные высших порядков для основных элементарных функций.
Пусть
функция y=f(x)
дифференцируема в точке Xo,
то существует ее производная в этой
точке f
’ (Xo).
Пусть f
- дифференцируема в некоторой окрестности
U(Xo).
f’(x)
определена на U(Xo)
и если дифференцируема в точке Xo,
то (f’(Xo))’=f’’(Xo).
Вообще
Производные основных элементарных функций
Билет 10
Формула Лейбница.
Теорема: (Формула Лейбница)
Пусть
функции U
и V
n
раз дифференцируемы, т.е. существуют
и
.
Значит (U*V)
– тоже n
раз дифференцируема, при этом
Доказательство:
Метод математической индукции:
Пусть при n=m – верно, т.е.
(*)
Надо доказать, что
Доказательство:
Теорема доказана.
Билет 11
Дифференциалы высших порядков. Неинвариантность формы дифференциалов высших порядков.
f(x)
дифференцируема,
тогда
.
Далее, пусть f
– n
раз
дифференцируема,
__________________________
.
Докажем, что
1)
,
2) Пусть при
n
= m
3)
Инвариантность/Неинвариантность.
1) y(x), x – независимая переменная, , пусть x = x(t)
2) y(x), x – независимая переменная, , ,
, здесь , .
Билет 12