Интегрирование рациональных дробей.

Пусть нужно найти неопределенный интеграл от рациональной действительной дроби. Если степень многочлена P k не меньше степени многочлена Q n ( ), то прежде всего разделим P на Q :

Многочлен R интегрируется без труда, а – правильная действительная дробь. Все трудности сводятся к интегрированию правильной дроби, которую мы снова обозначим через и представим в виде:

Тогда пусть ,

1 случай.

Знаменатель содержит простые действительные корни, тогда его можно разложить на простейшие множители: (см.Теор.1)

. Тогда

Приравнивая тождественно равные числители, получим:

Существуют 2 метода нахождения :

1. сравниваем коэффициенты при x с одинаковыми степенями; однако этот метод очень трудоемкий.

2. Т.к. равенства тождественны, можем взять , тогда 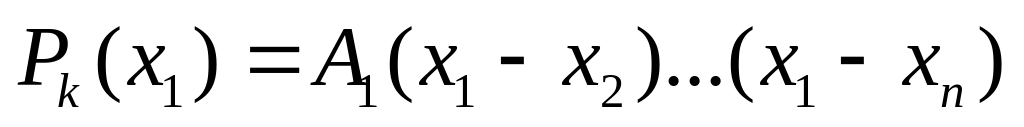. Так, подставляя поочередно найдем все

Т.о., мы получили сумму элементарных дробей, которые можем легко проинтегрировать.

Пример

2 случай.

Знаменатель содержит кратные корни, тогда его можно представить в виде:

.

Пусть существуют n различных корней с кратностями , тогда

- и делаем все так же, как и в предыдущем примере.

Пример

3 случай.

Знаменатель содержит кратные корни и многочлены, имеющие комплексные корни;

, где многочлены , имеют комплексные корни.

Тогда R(x) представим в виде:

Снова приводим к общему знаменателю и приравниваем числители.

Пример

4 случай

Знаменатель содержит кратные действительные и кратные комплексные корни;

Тогда R(x) представим в виде:

А дальше все делаем по старой схеме: методом неопределенных коэффициентов находим A, B...

Пример

Билет 33

Интегрирование тригонометрических выражений.

Пусть , где и - многочлены от u и v.

1) Если один из многочленов , четный по , а другой – нечетный по , то подстановка рационализирует интеграл.

2) Если один из многочленов , четный по , а другой – нечетный по u, то подстановка рационализирует интеграл.

3) Если оба многочлена четные по u и , то подстановка рационализирует интеграл.

3’) Выражения вида , где и - четные. Они сходны с 3 случаем, где

4) Универсальная подстановка.

Рационализация также достигается с помощью подстановки , которая называется универсальной. В самом деле,

; ;

.

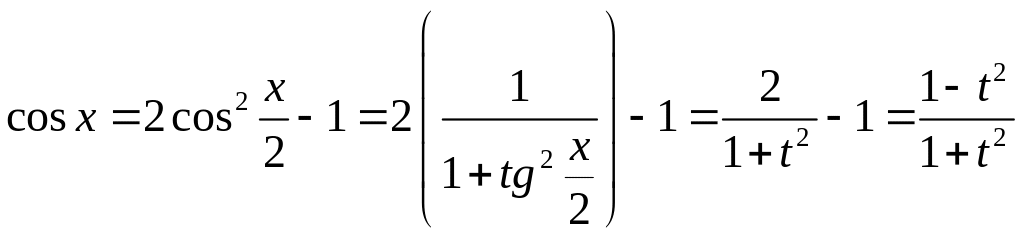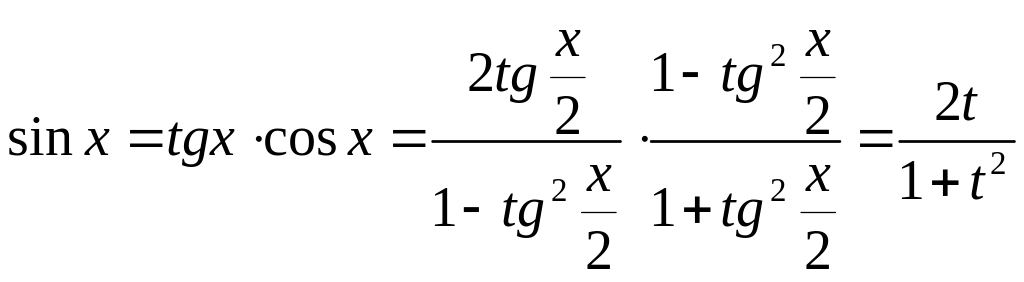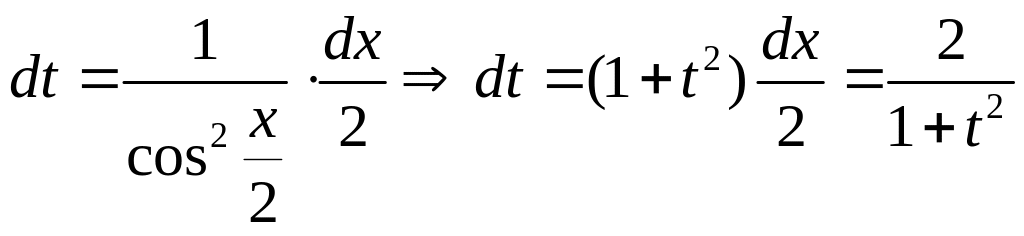
5) Выражения вида ; ; . Они рационализируются с помощью перевода в тригонометрические суммы.

Билет 34

Первая подстановка Эйлера (Леонарда)

Пусть многочлен имеет вещественные корни.

Пусть - корни, тогда .

Рассмотрим подстановку

Вторая подстановка Эйлера для интегралов вида , где .

Корни трехчлена ax2+bx+c комплéксные. Тогда надо считать, что a>0, иначе трехчлен был бы отрицателен для всех x. Делаем подстановку .Возводя это равенство в квадрат и заменяя его выражением, получим:

Где x, y и dx – некоторые рациональные функции от t. В конечном счете получаем:

.

Билет 35

Интегрирование выражений вида .

Докажем, что любой такой интеграл – берущийся в элементарных функциях. Пусть , т.к. . Пусть m=НОК , . Сделаем замену: , тогда , причем последнее выражение - рациональное, т.к. m делится на любое .

Тогда получим, что x=φ(t), dx=φ΄(t)dt, где φ(t) и φ΄(t)dt – рациональные выражения, поэтому: - тоже рациональное выражение

Билет 36