Пособие для подготовки к 1 сессии по матанализу Составлено на основе: лекции Соколовой Т.В. МИЭТ, 2003, 2009г.г. «Дифференциальное и интегральное исчисление», Бугров, Никольский

Билет 1

Модуль непрерывности. Равномерная непрерывность функции на множестве.

Функция f(x) задана на промежутке A, ω – модуль непрерывности

ω(δ) = sup| f(x₁) – f(x₂)| x₁, x₂  A, | x₁ – x₂ | < δ

1) ω(δ) > 0

2) δ1 < δ₂

ω(δ₁) = sup| f(x₁) – f(x₂)| x₁, x₂  A, | x₁ – x₂ | < δ₁ => | x₁ – x₂ | < δ₂

ω(δ₂) = sup| f(x₁) – f(x₂)| x₁, x₂  A, | x₁ – x₂ | ≤ δ₂

Но если x < y, то sup x < sup y => ω(δ₁) < ω(δ₂), т.е.  .

Определение 1. Если , то f(x) – называется равномерно непрерывной на множестве А.

f(x) – непрерывна на А, если:

 x₁  A   > 0  δ(x₁, )  x₂  A | x₁ – x₂ | < δ => | f(x₁) – f(x₂)| < .

Определение 2. f(x) – равномерно непрерывна на А, если   > 0  δ()  x₁, x₂  A

| x₁ – x₂ | < δ => | f(x₁) – f(x₂)| < 

Определение 1  Определение 2

Определение 2 => Определение 1:

 x₁, x₂  A   > 0 | x₁ – x₂ | < δ => | f(x₁) – f(x₂)| < , ω(δ) = sup| f(x₁) – f(x₂)|  .

Определение 1 => Определение 2:

ω(δ)  0, sup| f(x₁) – f(x₂)|  0, где | x₁ – x₂ | < δ   > 0  δ₁ > 0  δ 0 < δ < δ₁ => ω(δ) < 

 x₁, x₂ | x₁ – x₂ | < δ => | f(x₁) – f(x₂)| < .

Билет 2

Равномерная непрерывность функции, непрерывной на отрезке

Теорема. Функция непрерывная на отрезке равномерно непрерывна на нем.

Доказательство. Пусть f непрерывна, но не равномерна

  > 0  δ > 0  x₁, x₂ | x₁ – x₂ | < δ  | f(x₁) – f(x₂)| ≥ 

Возьмем δ= ,  x’_n, x”_n | x’_n – x”_n | < δ  sup| f(x’_n) – f(x”_n)| ≥ 

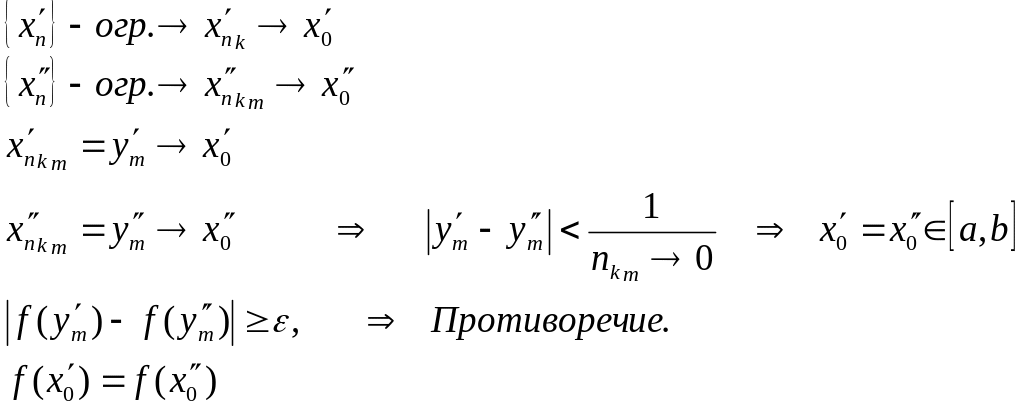
Билет 3

Производная. Определение, непрерывность функции, имеющей производную. Геометрический смысл производной.

Определение: Производной от функции в точке называется предел, к которому стремится отношение ее приращения в этой точке к соответствующему приращению аргумента, когда последнее стремится к нулю:

Т.е., если определена в , то

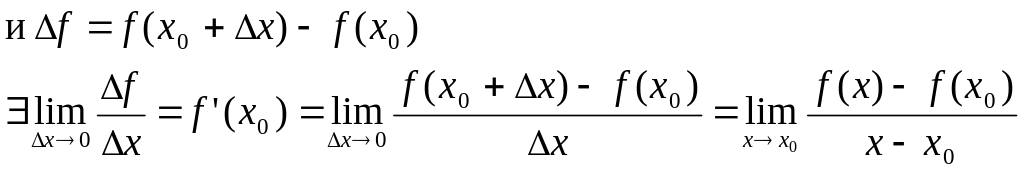
Теорема: (необходимое условие существования производной)

Если функция имеет конечную в точке , то непрерывна в точке .

Доказательство:

При ,

Следовательно - непрерывна в точке .

Теорема доказана.

Замечание: обратное утверждение неверно, если функция непрерывна в точке , то отсюда не следует, что она имеет производную в этой точке.

Контрпример:

Утверждение: если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева.

Контрпример:

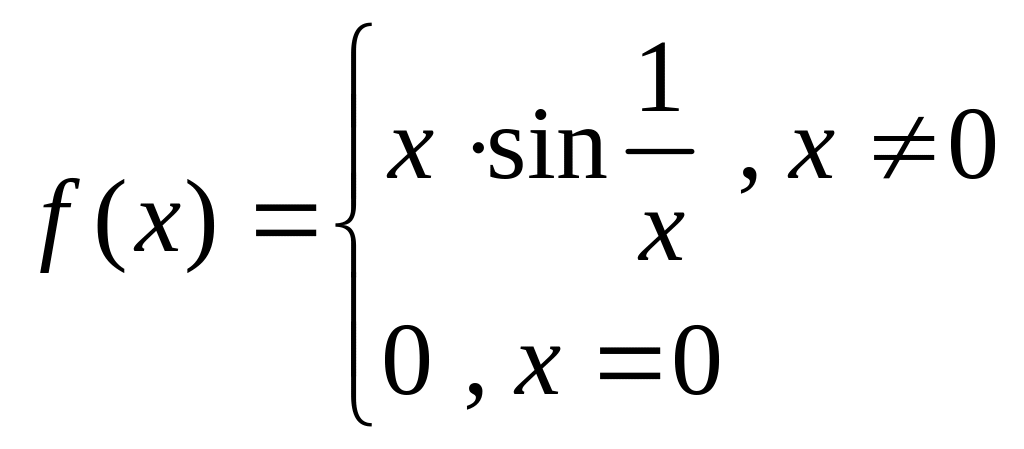
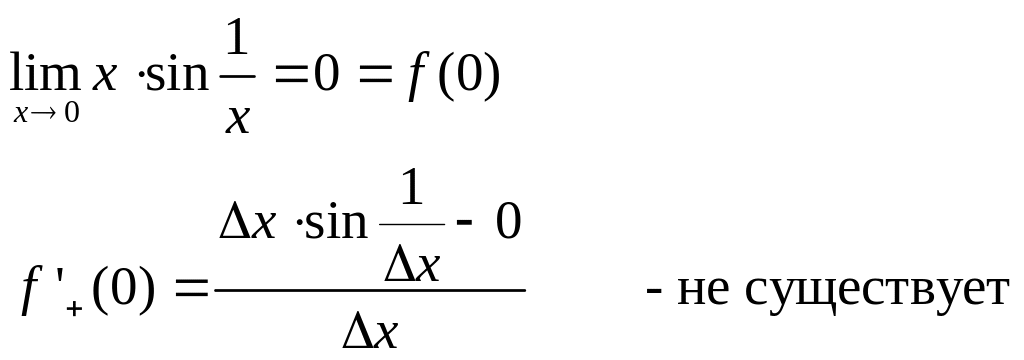
Геометрический смысл производной.

Теорема 1:

График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.

Д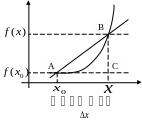 оказательство:

Пусть существует значение f’( )-конечное, тогда

при

Секущая стремится к касательной.

=> ч.т.д.

Пусть существует невертикальная касательная => существует - конечный.

Секущая стремится к касательной.

=>

Теорема доказана.