[Править] Пример

Для решения следующей системы уравнений:

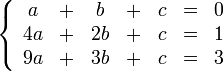
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

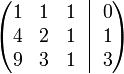
Проведём следующие действия:

• К строке 2 добавим: −4 × Строку 1.

• К строке 3 добавим: −9 × Строку 1.

Получим:

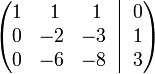
• К строке 3 добавим: −3 × Строку 2.

• Строку 2 делим на −2

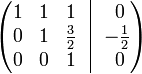
• К строке 1 добавим: −1 × Строку 3.

• К строке 2 добавим: −3/2 × Строку 3.

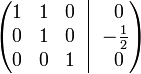
• К строке 1 добавим: −1 × Строку 2.

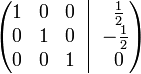
В правом столбце получаем решение:

.

10

Однородные системы линейных уравнений

     Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.

     Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

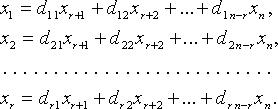
     Тогда n - r линейно независимыми вектор-решениями будут:

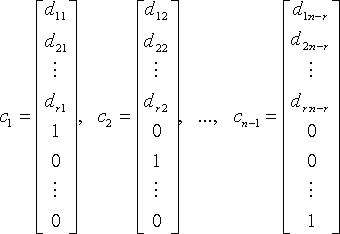
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

     В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.

11

12

13

Едини́чныйве́ктор или орт (единичный вектор нормированного векторного пространства) — вектор, норма (длина) которого равна единице.

Единичный вектор  , коллинеарный с заданным   (нормированный вектор), определяется по формуле

.

В качестве базисных часто выбираются именно единичные векторы, так как это упрощает вычисления. Такие базисы называют нормированными. В том случае, если эти векторы такжеортогональны, такой базис называется ортонормированным базисом.

Углом между двумя ненулевыми векторами   и   называется наименьший угол  ( ), на который надо повернуть один из векторов до его совпадения со вторым. Предварительно нужно привести векторы к общему началу О (рис. 7).

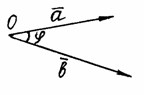
Рис. 7

Под углом между вектором   и осью   понимают угол между векторами   и   (рис. 8).

 

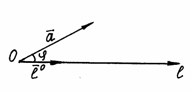
Рис. 8

Пусть   – некоторая ось, а   – вектор, произвольно распо-ложенный в пространстве. Обозначим   и   – проекции на ось   соответственно начала А и конца В этого вектора (рис. 9). Вектор  называется составляющей вектора   по оси  .

 

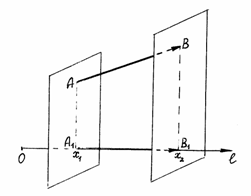
Рис. 9

Проекцией вектора   на ось   (обозначается пр ) называется длина его составляющей   по этой оси, взятая со знаком «плюс», если  , и со знаком «минус», если  .

Очевидно, что пр , если вектор   образует острый угол с осью  ; пр , если этот угол тупой; пр , если  .

Если известны координаты точек   и   на оси:  ,  , то пр .

Нетрудно доказать свойства проекций:

1)     Равные векторы имеют равные проекции на одну и ту же ось.

2)     пр пр пр .

3)     пр пр ,  .

4)     пр , где   – угол между вектором и осью.

Заметим, что проекция вектора на ось и его составляющая связаны соотношением сост пр .

Пример 1. При каком условии  ?

Решение. Отнесем векторы   и   к общему началу О и построим на них параллелограмм (рис.5). Тогда   – длина диагонали ОС этого параллелограмма, а   – длина диагонали ВА. Диагонали параллелограмма равны, если этот параллелограмм – прямоугольник. Следовательно,  , если  .

. Если   - векторы, по модулю равные единице и направленные по координатным осям Ox, Oy и Oz, то разложение вектора   по трем координатным осям выражается формулой

     (10)

где a_x, a_y и a_z - проекции вектора a на координатные оси - называются координатами вектора (если вектор   имеет координаты a_x, a_y, a_z, то это обозначается так:  {a_x, a_y, a_z}). Если вектор   имеет начало в начале координат, а его конец A имеет координаты x, y и z, то тогда его проекции на координатные оси равны координатам его конца:

a_x = x; a_y = y; a_z = z.

В этом случае вектор   называется радиусом-вектором точки A. Радиус-вектор точки обозначается обыкновенно через   (см. рисунок):

     (11)

а модуль радиуса-вектора точки A(x, y, z) вычисляется по формуле

     (12)

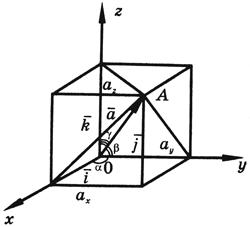
Разложение вектора по базису.

Определение. Пусть  – произвольный вектор,  – произвольная система векторов. Если выполняется равенство

                   ,                       (1)

то говорят, что вектор  представлен в виде линейной комбинации данной системы векторов. Если данная система векторов  является базисом векторного пространства, то равенство (1) называется разложением вектора  по базису . Коэффициенты линейной комбинации  называются в этом случае координатами вектора  относительно базиса .

Теорема. (О разложении вектора по базису.)

Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.

   Доказательство. 1) Пусть L произвольная прямая (или ось) и – базис . Возьмем произвольный вектор . Так как оба вектора  и  коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что  и тем самым мы получили разложение вектора  по базису  векторного пространства .

   Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису  векторного пространства :

 и , где . Тогда  и используя закон дистрибутивности, получаем:

                       .

Так как , то из последнего равенства следует, что , ч.т.д.

2) Пусть теперь Р произвольная плоскость и  – базис . Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую , на которой лежит вектор , прямую , на которой лежит вектор . Через конец вектора  проведем прямую параллельную вектору  и  прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма , и , ,  – базис ,  – базис .

   Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа , что

   и . Отсюда получаем:

 и возможность разложения по базису доказана.

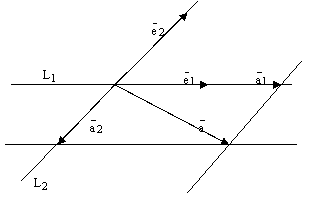
                                         рис.3.

   Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора  по базису  векторного пространства :  и . Получаем равенство

, откуда следует . Если , то , а т.к. , то  и коэффициенты разложения равны: , . Пусть теперь . Тогда , где . По теореме о коллинеарности двух векторов отсюда следует, что . Получили противоречие условию теоремы. Следовательно,  и , ч.т.д.

3) Пусть – базис  и пусть  произвольный вектор. Проведем следующие построения.

Отложим все три базисных вектора  и вектор  от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы , плоскость  и плоскость ; далее через конец вектора  проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

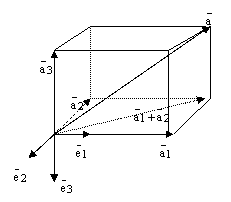
                             рис.4.

По правилу сложения векторов получаем равенство:

                        .                                    (1)

По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число , такое что . Аналогично,  и , где . Теперь, подставляя эти равенства в (1), получаем:

                                             (2)

 и возможность разложения по базису доказана.

   Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису :

 и . Тогда

       .       (3)

   Заметим, что по условию векторы   некомпланарные, следовательно, они попарно неколлинеарные.

Возможны два случая:  или .

а) Пусть , тогда из равенства (3) следует:

           .                        (4)

Из равенства (4) следует, что вектор  раскладывается по базису , т.е. вектор  лежит в плоскости векторов  и, следовательно, векторы  компланарные, что противоречит условию.

б) Остается случай , т.е. .  Тогда из равенства (3) получаем  или

             .                           (5)

Так как – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что  и , ч.т.д.

14