3. Сложение одинаково направленных гармонических колебаний с одинаковыми частотами. Метод векторной диаграммы. Биения.

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты.

П остроим векторные диаграммы этих колебаний (рис.). Т.к. векторы A₁ и A₂ вращаются с одинаковой угловой скоростью ω_0, то разность фаз (φ₂ – φ₁) между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет:

В предыдущем выражении амплитуда А и начальная фаза φ соответственно задаются соотношениями:

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и стой же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ₂ – φ₁) складываемых колебаний.

Проанализируем вышенаписанное выражение в зависимости от разности фаз (φ₂ – φ₁):

1. , тогда А=А₁+А₂, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2. , тогда , т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.

Биения – периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.

Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+∆ω, причем . Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

С кладывая эти выражения и учитывая, что во втором сомножителе , найдем Данное результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда которого изменяется по следующему периодическому закону:

Частота изменения в два раза больше частоты изменения косинуса (т.к. берется по модулю), т.е. частота биений равна разности частот складываемых колебаний: Период биений: .

Характер зависимости показан на рис., где сплошные жирные линии дают график результирующего колебания, а огибающие их – график медленно меняющейся по уровню амплитуды.

Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.

4. Сложение взаимно-перпендикулярных колебаний. Фигуры Лиссажу.

Материальная точка может одновременно участвовать в нескольких колебательных процессах. Рассмотрим один из простейших случаев: точка участвует в двух колебаниях одинаковых частот, совершаемых по взаимно- перпендикулярным направлениям – осям OX и OY. Уравнения этих колебаний:

x = A₁ sinωt; (1)

y = A₂ sin(ωt + φ), (2)

где x и y – смещения колеблющейся точки по осям OX и OY соответственно; A₁ и A₂ – амплитуды складываемых колебаний. Для упрощения последующих математических преобразований начальная фаза первого из складываемых колебаний выбрана равной нулю, тогда начальная фаза φ второго колебания равна разности фаз колебаний: φ = φ₂ – φ_1. (3)

Из уравнения (1): sinωt = x/A₁, (4)

тогда cosωt = (5)

Из уравнения (2): sin(ωt + φ) = y/A₂.

Воспользовавшись известной тригонометрической формулой:

sin(α + β) = sinα cosβ + cosα sinβ,

запишем: sinωt cosφ + cosωt sinφ = y/A₂.

Подставим в полученное уравнение значения sinωt и cosωt из уравнений (4) и (5):

Перепишем полученное уравнение в виде:

и возведем его в квадрат:

Проделаем несложные математические преобразования:

Поскольку запишем:

Получено уравнение эллипса в канонической его форме. Подставим значение φ = φ₂ – φ₁:

(6)

Таким образом, можно сделать вывод, что в общем случае точка, участвующая в двух взаимно перпендикулярных колебаниях одинаковых частот. Движется по эллиптической траектории, такой, например, как показана на рис.1.

Некоторые частные случаи.

1. Начальные фазы складываемых колебаний одинаковы: φ = φ₂ – φ₁=0_.

При этом уравнение (6) принимает вид:

откуда следует, что или (7)

Получено уравнение прямой, проходящей через начало координат (прямая 1 на рис.2).

2. При разности фаз: φ = φ₂ – φ₁=±π.

Уравнение (6) принимает вид: (8), откуда следует, что Это уравнение прямой 2 на рис.2.

3. Разность фаз φ = φ₂ – φ₁=±π/2.

Уравнение (6) принимает вид:

П олучено уравнение эллипса, приведенного к координатным осям OX и OY (рис.3, кривая 1).

Если при этом амплитуды складываемых колебаний одинаковы (A₁=A₂=A), то уравнение преобразуется в уравнение окружности (кривая 2, рис.3.): (10)

При сложении колебаний разных частот точка движется по сложной, непрерывно изменяющейся траектории.

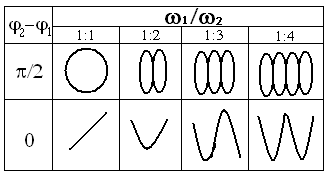
Однако при сложении колебаний кратных частот траектории принимают довольно простую форму, зависящую от соотношения частот и разности фаз складываемых колебаний. Эти кривые носят название фигур Лиссажу. Вид фигур Лиссажу для отношений частот 1:1, 1:2, 1:3, 1:4 показан в таблице.