- •1. Гармонический осциллятор, его закон движения, скорость, ускорение, возвращающая сила, энергия.
- •2. Маятники пружинный, математический, физический.
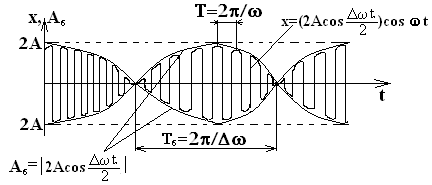
- •3. Сложение одинаково направленных гармонических колебаний с одинаковыми частотами. Метод векторной диаграммы. Биения.
- •4. Сложение взаимно-перпендикулярных колебаний. Фигуры Лиссажу.
- •5. Свободные затухающие колебания. Логарифмический декремент. Апериодический процесс.
- •6. Вынужденные колебания. Резонанс
- •7. Волна, уравнение гармонической волны.
- •8. Перенос волной энергии, вектор Умова.
- •9. Электромагнитное поле. Уравнения Максвелла. Плоская электромагнитная волна.
- •Уравнения Максвелла для электромагнитного поля
- •Интерференция волн
- •Интерференция света
- •11. Интерференция света в тонких пленках, примеры ее наблюдения и применения.
- •Кольца Ньютона
- •Полосы равного наклона (интерференция от плоскопараллельной пластинки)
- •Применение интерференции света
- •12. Дифракция, условие её наблюдения. Принцип Гюйгенса-Френеля. Метод зон Френеля и его применение для расчета дифракции света на узкой щели.
- •13. Дифракционная решетка, ее применение в качестве спектрального прибора.
- •14. Физические принципы голографии.
- •15. Поляризация света. Поляризатор и анализатор. Закон Малюса. Примеры получения и применения поляризованного света.
- •16. Тепловое излучение, его характеристики: энергетическая светимость, испускательная и поглощательная способности. Цвет несамосветящегося тела. Абсолютно черное и серое тела. Закон Кирхгофа
- •17. Законы излучения абсолютно черного тела: Закон Стефана-Больцмана, закон Вина. Трудности классической физики при объяснении распределения энергии в спектре черного тела. Квантовая гипотеза Планка.
- •1. Закон Стефана-Больцмана:
- •2. Закон Вина:
- •18. Фотоэффект, красная граница, работа выхода электрона из металла, задерживающее напряжение. Квантовый механизм фотоэффекта, уравнение Эйнштейна.
- •19. Эффект Комптона, его квантовый механизм.
- •20. Корпускулярно-волновой дуализм излучения. Фотоны. Взаимосвязь волновых и корпускулярных характеристик фотонов. Связь между корпускулярной и волновой картинами.
- •21. Волна де Бройля. Дифракция электронов. Статистический смысл волн де Бройля. Электронный микроскоп как пример практического использования электронных волн.
- •22. Соотношения неопределенностей как выражение корпускулярно-волнового дуализма и границ применения классической физики.
- •23. Состояние и уравнение движения квантовой частицы. Волновая функция, ее статистический смысл. Уравнение Шредингера.
- •24. Примеры применения уравнения Шредингера: частица в бесконечно глубокой потенциальной яме; гармонический осциллятор.
- •25. Развитие представлений о строении атома. Модель атома Резерфорда, ее недостатки.
- •26. Спектры испускания и поглощения атомов как источник информации об их строении и свойствах. Спектр атома водорода. Формула Бальмера.
- •27. Модель атома Бора, ее недостатки. Постулаты Бора. Энергетические уровни атома водорода и его спектр по модели Резерфорда – Бора.
- •28. Волновая модель атома водорода. Квантовые числа, их проявления в опыте. Периодическая таблица элементов Менделеева как отражение квантовых состояний электронов.
- •29. Спонтанное и вынужденное излучение. Лазер.
- •30. Ядро атома: состав, размеры, плотность. Энергия связи ядра атома, удельная энергия связи.
- •31. Радиоактивность. Закон радиоактивного распада. Период полураспада. Виды радиоактивного распада. Экологические аспекты радиоактивности.
- •32. Ядерная реакция. Законы сохранения. Энергетический эффект. Реакция деления тяжелых ядер, термоядерная реакция, их применение в энергетике, экологические аспекты.
1. Гармонический осциллятор, его закон движения, скорость, ускорение, возвращающая сила, энергия.
Гармонический
осциллятор
– система, совершающая колебания,
описываемые дифференциальным уравнением
гармонических колебаний:
![]() .
Решением этого уравнения является
выражение:
.
Решением этого уравнения является
выражение:
![]() (*), где A
– максимальное значение колеблющейся
величины (амплитуда колебания), ω0
– круговая (циклическая) частота, φ
– начальная фаза колебания в момент
времени t=0,
(ω0t
+ φ) – фаза
колебания в момент времени t.
Фаза колебания определяет значение
колеблющейся величины в момент времени
t.
Так как косинус изменяется в пределах
от +1 до -1, то s
может принимать значения от
+А до
–А.
(*), где A
– максимальное значение колеблющейся
величины (амплитуда колебания), ω0
– круговая (циклическая) частота, φ
– начальная фаза колебания в момент
времени t=0,
(ω0t
+ φ) – фаза
колебания в момент времени t.
Фаза колебания определяет значение
колеблющейся величины в момент времени
t.
Так как косинус изменяется в пределах
от +1 до -1, то s
может принимать значения от
+А до
–А.
За период колебаний
фаза колебания получает приращение 2π,
т.е.:
![]()
![]() откуда:
откуда:
![]()
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

Из последнего
выражения и следует дифференциальное
уравнение гармонических колебаний
![]() .
.
Пусть материальная
точка совершает прямолинейные
гармонические колебания вдоль оси
координат х
около положения
равновесия, принятого за начало координат.
Тогда зависимость координаты х
от времени
t
задается уравнением, аналогичным
уравнению (*), где s=x:
![]()
Скорость и ускорение – это первая и вторая соответственно производные от х:

Сила F = ma, действующая на колеблющуюся м.т. массой m вышенаписанных уравнений, равна:
![]() где
где
![]() .
.
Кинетическая
энергия
![]() м.т., совершающей прямолинейные
гармонические колебания равна:
м.т., совершающей прямолинейные
гармонические колебания равна:
![]() или
или
![]()
Потенциальная
энергия
![]() м.т., совершающей гармонические колебания
под действием упругой силы F,
равна
м.т., совершающей гармонические колебания
под действием упругой силы F,
равна
![]() или
или
![]()
Полная энергия
Е:
![]() .
.![]()
ВЫВОДЫ:
1. Колебания возникают при условии: а)
положения равновесия
![]() б) возвращающая сила
б) возвращающая сила
![]() в) инертность, m.
2.
в) инертность, m.
2.
![]() где ψ
- колеблющаяся
величина (x,
v,
A,
F).
где ψ
- колеблющаяся
величина (x,
v,
A,
F).
Если уравнение
движения имеет такой вид, то это
гармонические колебания с
![]() .
.
Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.
2. Маятники пружинный, математический, физический.
1. Пружинный
маятник –
это груз массой m,
подвешенный на абсолютно-упругой пружине
и совершающий гармонические колебания
под действием упругой силы
![]() ,
где k
– жесткость пружины. Уравнение движения
маятника:
,
где k
– жесткость пружины. Уравнение движения
маятника:
![]() или
или
![]()
П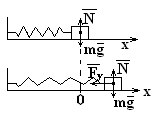 ружинный
маятник совершает гармонические
колебания по закону:
ружинный
маятник совершает гармонические
колебания по закону:
![]() с циклической частотой
с циклической частотой
![]() и периодом
и периодом
![]()
Потенциальная
энергия пружинного маятника:
![]()
2 .
Физический маятник –
это твердое тело, совершающее под
действием силы тяжести вокруг неподвижной
горизонтальной оси, проходящей через
точку О,
не совпадающую с центром масс С.
.
Физический маятник –
это твердое тело, совершающее под
действием силы тяжести вокруг неподвижной
горизонтальной оси, проходящей через
точку О,
не совпадающую с центром масс С.
Если маятник
отклонен от положения равновесия на
некоторый
угол
α, то в
соответствии с уравнением динамики
вращательного движения твердого тела:
![]() момент М
возвращающей
силы можно записать в виде:
момент М
возвращающей
силы можно записать в виде:
![]() ,
где J
– момент инерции маятника относительно
оси, проходящей через точку подвеса О,
l
– расстояние между ней и центром масс
маятника, Fτ
- возвращающая
сила.
,
где J
– момент инерции маятника относительно
оси, проходящей через точку подвеса О,
l
– расстояние между ней и центром масс
маятника, Fτ
- возвращающая
сила.
Запишем предыдущее
уравнение в виде:
![]() или
или
![]() Принимая
Принимая
![]() получим уравнение
получим уравнение
![]() (гармонический осциллятор), решение
которого:
(гармонический осциллятор), решение
которого:
![]()
Период физического
маятника:
![]() ,
где
,
где
![]() -приведенная
длина физического маятника.
-приведенная
длина физического маятника.
3. Математический маятник – это идеализированная система, состоящая из м.т. массой m,подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести.
М![]() омент
инерции математического маятника:
омент
инерции математического маятника:
![]() где l
–длина
маятника.
где l
–длина
маятника.
Т.к. математический
маятник можно представить, как частный
случай физического маятника, предположив,
что вся его масса сосредоточена в одной
точке – центре масс, то, подставив
формулу момента инерции в формулу
периода физического маятника, получим
выражение для периода малых колебаний
математического маятника:
![]()