5.2.4. Анализ цепей синусоидального тока первого порядка (rl и rc цепи)
5 .2.4.1. Последовательная rl-цепь
Схема ЭЦ показана
на рис.5.14. Согласно II
закона Кирхгофа состояние цепи
описывается выражением
=
+
=
(R+jωL)=
,
где Z – полное комплексное сопротивление цепи, модуль (полное сопротивление) и аргумент (фаза) которого равны соответственно:
,
argZ=φ=
.
(5.8)
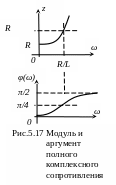Графики этих
зависимостей показаны на рис.5.17.
На рис.5.15 изображена
векторная диаграмма комплексов тока и
напряжений ЭЦ, причем комплексы тока и
напряжения на резистивном элементе в
данном случае приняты вещественными
величинами, т.к. векторы их совпадают с
вещественной осью (
=
,
=
).
На рис.5.16 отображены временные диаграммы
реальных напряжений в ЭЦ. Как видно из
рисунков напряжение на входе цепи
опережает ток в цепи на угол φ.
5.2.4.2. Параллельная rl-цепь
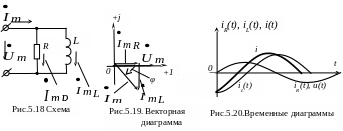
Схема ЭЦ показана на рис.5. 18. Согласно I закона Кирхгофа состояние цепи описывается выражением:
=
+
=
,
где Z=
– полное комплексное сопротивление
цепи, модуль (полное сопротивление) и
аргумент (фаза) которого равны
соответственно:
z(ω)
=
,
argZ=φ=
.
(5.9)
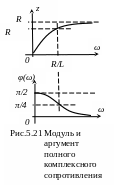Графики
зависимостей (5.9) показаны на рис.5.21.
На рис.5.19 изображена векторная диаграмма комплексов тока и напряжений ЭЦ, причем комплексы тока и напряжения на резистивном элементе в данном случае приняты вещественными величинами, т.е. векторы их совпадают с вещественной осью ( = , = ). На рис.5.20 отображены временные диаграммы реальных токов в ЭЦ. Как видно из рисунков, также как и в предыдущем случае, напряжение на входе цепи опережает ток в цепи на угол φ.
5.2.4.3. Последовательная rс-цепь
Схема ЭЦ показана на рис.5.22. Согласно II закона Кирхгофа состояние цепи описывается выражением
=
+
=
(R-
)=
,
где Z – полное комплексное сопротивление цепи, модуль (полное сопротивление) и аргумент (фаза) которого равны соответственно:
,
argZ=φ=
-
.
(5.10)
Г
рафики
зависимостей модуля и аргумента показаны
на рис.5.25. На рис.5.23 изображена векторная
диаграмма комплексов тока и напряжений
ЭЦ, причем комплексы тока и напряжения
на резистивном элементе в данном случае
приняты вещественными величинами, т.е.
векторы их совпадают с вещественной
осью (
=
,
=
).
На рис.5.24 изображены временные диаграммы
тока и реальных падений напряжения в
ЭЦ. Как видно из рисунков, напряжение
на входе цепи отстает от тока в цепи на
угол φ.
5 .2.4.4. Параллельная rс-цепь
Схема ЭЦ показана
на рис.5.26. Согласно I
закона Кирхгофа состояние цепи описывается
выражением
=
+
=
=
,
где полное комплексное сопротивление
цепи -
Z
=
;
его модуль (полное сопротивление) и
аргумент (фаза) равны соответственно:
,
argZ=φ=
-
.
(5.10)
Г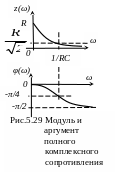
рафики
зависимостей модуля и аргумента показаны
на рис.5.29. На рис.5.27 изображена векторная
диаграмма комплексов тока и напряжений
ЭЦ, причем комплексы тока и напряжения
на резистивном элементе в данном случае
приняты вещественными величинами, т.е.
векторы их совпадают с вещественной
осью (
=
,
=
).
На рис.5.28 изображены временные диаграммы
тока и реальных падений напряжения в
ЭЦ. Как видно из рисунков, напряжение
на входе цепи отстает от тока в цепи на
угол φ.