3.4. Метод наложения (суперпозиции)

Метод основан на принципе суперпозиции , обусловленным линейно­стью электрической цепи. Если линейная цепь подвергается воздействию одновременно нескольких источников, то реакция цепи равна сумме реак­ций на каждое воздействие отдельно. Тогда принцип наложения можно сформулировать следующим образом: ток в любой ветви ЭЦ равен сумме токов, обусловленных в отдельности каждым источником, действующим в отсутствии остальных; напряжение между двумя точками ветви равно сумме напряжений, обусловленных в отдельности каждым источником, действующим в отсутствии остальных.

3.4.1. Алгоритм расчета тока в k-той ветви (напряжения между точками «а» - «б» в k-той ветви).

I. Получают столько L частичных схем, сколько в исходной схеме ЭЦ ис­точников (ИИН и ИИТ).

II. В каждой частичной схеме оставляют один источник, заменяя осталь­ные их внутренними сопротивлениями [0 для ИИН, ∞ (разрыв) для ИИТ].

III. Рассчитывается ток k-той ветви - I_kl (напряжение Uаб_kl в k-той ветви) каждой l-ной частичной схемы.

IV. Рассчитывается ток k-той ветви - I_k (напряжение Uаб_k в k-той ветви):

I_k = . Uаб_k = , руководствуясь правилом знаков – если направления токов (напряжений) в полной и частичной схеме совпадают, то токи (напряжения) берутся со знаком «+», если не совпадают – со знаком «-».

Пример 8

Рассчитать ток ветви а-б схемы рис.3.4 методом наложения.

Д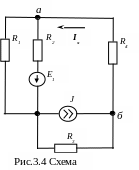 ано:

Е1, В	J, А	R1, Ом	R2, Ом	R3, Ом	R4, Ом
50	0,2	50	150	60	70

Расчет.

Поскольку исходная схема содержит два источника, ток I_х будет определяться как суперпозиция токов I_х = I_х` ± I_х`` ветви а-б двух частичных схем (рис.3.5 и рис.3.6).

1. Расчет тока I_х` осуществляется с ис­пользование правила делителя тока, так как ток J разветвляется по двум ветвям:

I_х` = .

2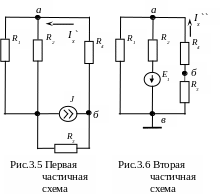 . Для расчета тока I_х`` можно воспользоваться методом узловых потен­циалов при условии, что потенциал точки «в» ра­вен нулю, тогда ток

I_х`= .

Согласно МУП потен­циал φ_а определяется из уравнения

Подставив числовые значения получаем:

I_х = I_х` ± I_х``= 0,34 А

Пример 9

Рассчитать напряжение U_аб схемы рис.3.7 методом наложения.

Д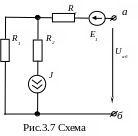 ано:

Е1, В	J, А	R1, Ом	R2, Ом	R3, Ом
50	0,2	50	150	60

Расчет:

Поскольку исходная схема содержит два источника, напряжение U_аб будет оп­ределяться как суперпозиция напряжений U_аб = U_аб`± U_аб``для двух частичных схем (рис.3.8 и рис.3.9).

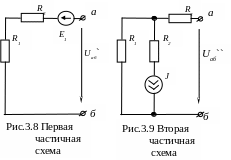Очевидно, что напряжение U_аб`= -Е₁, поскольку источник Е₁ работает в режиме Х.Х. и точка «а» имеет отрицательный потенциал.

Напряжение

U_аб``= - J R₁ = -10 В.

Таким образом, напряжение U_аб=-60В.

3.5. Метод эквива­лентного генератора

Метод применяется в том случае, когда необходимо рассчи­тать ток какой-либо ветви сложной схемы. Ветвь с искомым током I_X (рис.3.10) представляется нагрузкой активного двухполюсника (АД), который заменяет собой всю остальную схему ЭЦ. АД в свою очередь реализуется в виде реального источника напряжения (РИН), величина ЭДС которого равна напряжению холостого хода на зажимах 1-2 АД, а внутреннее сопротивление - вход­ному сопротивлению этого АД. Напряжение холостого хода можно рассчитать любым из известных методов расчета схемы ЭЦ, для расчета же входного сопротивления необходимо превратить АД в пассивный двухполюсник, для чего заменить в нем идеальные источники энергии их внутренними сопротивлениями (ИИН - 0; ИИТ - ∞).

Пример 10

Рассчитать ток ветви 2-4 схемы рис.3.11 используя метод эквивалент­ного генератора (ЭГ).

Дано:

Е1, В	Е2, В	J, А	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом
50	100	0,2	50	150	60	70	80

Расчет.

1. Расчет параметров ЭГ.

Расчет внутреннего сопротивления ЭГ производится по схеме рис.3.12, как входного сопротивления относительно зажимов 2-4 пассивного двухполюсника:

= 73,3 Ом.

Для расчета напряжения холостого хода целесообразно использовать метод наложения. Согласно методу - U₂₄ = U₂₄`± U<sub>24</sub>``, где U<sub>24</sub>`- напряже­ние между точками 2-4 первой частичной схемы, U₂₄``- напряжение между точками 2-4 второй частичной схемы. Для контура обхода схемы рис.3.13 имеет место следующее равенство: U<sub>24</sub>` - I(R<sub>2</sub>+R<sub>4</sub>)+E<sub>1</sub>= 0, где ток I = . U<sub>24</sub>` = =I(R<sub>2</sub>+R<sub>4</sub>)-E<sub>1</sub> = -16,6 В, Для контура обхода схемы рис.3.14 можно записать: U<sub>24</sub>`` + I₂R₄ – I₁R₂ = 0, откуда = I₁R₂ - I₂R₄ = Токи I₁ и I₂ определяются по правилу деления тока источника J:

= 0,079 А = 0,12 А.

U₂₄`` = 3,45 В. Итак, U_XXЭГ = U₂₄. = -13,15 В. Следует обратить внимание на то, что ЭДС ЭГ (Е_ЭГ) направлено от точки 2 к точке 4, т.к. U_XXЭГ – отрица­тельная величина.

2. Расчет искомого тока.

Согласно закону Ома для полной цепи:

I_Х = .

Подставив в полученные выражения числовые значения получаем:

I_Х = 0,566 А.