31. Геометрический смысл уравнения Бернулли

- уравнение Бернулли для элементарной струйки

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

Как и в гидростатике, величину Z называют нивелирной высотой.

Второе слагаемое - носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

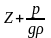
Сумма первых двух членов уравнения  гидростатический напор.

Третье слагаемое в уравнения Бернулли 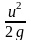называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

Значения 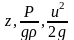- нивелирную, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек, высоты которых равны , называется пьезометрической линией. Если к этим высотам добавить скоростные высоты, равные , то получится другая линия, которая называется гидродинамической или напорной линией.

Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.

32. Гидравлический уклон. Диаграмма уравнения Бернулли

Гидравли́ческий укло́н — это величина, характеризующая собой потерю напора на единицу длины русла.

При постоянной скорости течения и одинаковой высоте русла (то есть, при горизонтальном русле) гидравлический уклон может быть определён по формуле: где H₁ — напор потока жидкости в начале участка русла; H₂ — напор потока жидкости в конце участка русла; l — длина участка русла.

Для ламинарного течения (течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления)  жидкости в трубах круглого сечения гидравлический уклон может быть определён по формуле: где λ — коэффициент потерь на трение по длине; Q — расход жидкости; D — диаметр трубы.

Для наклонных русел гидравлический уклон численно равен тангенсу угла, чуть меньшего, чеи угол наклона русла.

Гидравлический уклон играет важную роль при расчёте трубопроводов, канализационных труб, каналов и др.

На рисунке 1 приведена диаграмма уравнения Бернулли для потока реальной жидкости. Здесь 0—0 — плоскость сравнения; N—N — плоскость начального напора; Н—Н — напорная линия, или линия полной удельной энергии. Падение ее на единицу длины представляет гидравлический уклон J; Р—Р — пьезометрическая линия, или линия удельной потенциальной энергии. Падение ее на единицу длины представляет пьезометрический уклон J_п.

РИСУНОК 1

Так как общий запас удельной энергии вдоль потока непрерывно уменьшается, линия Н—Н всегда нисходящая, а гидравлический уклон всегда положительный (J>0). Пьезометрическая линия может быть и нисходящей, и восходящей (последнее имеет место на расширяющихся участках, когда средняя скорость потока уменьшается), поэтому пьезометрический уклон может быть и положительным (J>0), и отрицательным(J<0).

На участках с равномерным движением жидкости, где имеют место только потери напора на трение по длине, линии Н—Н и Р—Р представляют взаимно параллельные прямые, поэтому J = J_п =h_дл/L. В этом случае потеря напора может быть определена по разности гидростатических напоров:

h_дл = (z₁ + p₁/γ) - (z₂ + p₂/γ)

РИСУНОК 2

Для горизонтальных участков потоков (z₁=z₂) или в случае, если плоскость сравнения 0—0 проведена по оси потока (z₁=z₂=0) (рисунок 2), потеря напора на трение по длине может быть определена непосредственно по разности показаний пьезометров:

h_дл = (p₁ — p₂)/γ