
- •1. Обобщенные приемы познавательной деятельности процесса поиска решения задач: функциональный подход.
- •2. Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов на плоскости
- •3. Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов в пространстве
- •Установление области определения.
- •Установление области изменения при заданной области определения.
- •Установление способа движения по множеству значений, при указанном способе движения по области определения.
- •Обобщенные приемы познавательной деятельности процесса поиска решения задач: аналогия, обобщение, конкретизация.
- •5. Обобщенные приемы познавательной деятельности процесса поиска решения задач: Метод математической индукции
- •6 . Обобщенные приемы познавательной деятельности процесса поиска решения задач: использование классических неравенств.
- •7.Функциональный подход в поиске решений задач: использование монотонности.
- •8.Функциональный подход в поиске решений задач: ограниченность (метод крайнего).
- •9.Функциональный подход в поиске решений задач: четности.
- •10.Функциональный подход в поиске решений задач: решение задач, содержащих целую и дробную часть числа.
- •Виды задач
- •Методы решения
- •12. Олимпиадные задачи. Основы теории чисел: простые числа, алгоритм Евклида.
- •13.Олимпиадные задачи. Инварианты. Полуинварианты.
- •14. Олимпиадные задачи, решаемые с использованием принципа Дирихле.
- •15. Комбинаторные задачи, приемы и методы их решения
- •16. Задачи на раскраски, укладки, замощения.
- •17. Диофантовы уравнения.
- •18. Логические задачи, решаемые с помощью графов
- •19. Логические задачи, решаемые с помощью составления таблиц истинности.
- •20. Олимпиадные задачи с геометрическим содержанием
- •21. Задачи - игры
- •22. Олимпиадные задачи с параметрами. Методы их решения.
- •23. Применение векторов к решению аффинных задач в пространстве.
- •24.Применение векторов к решению метрических задач в пространстве.
- •25.Векторно-координатный метод определения угла между прямыми.
- •Алгоритм векторно-координатного метода:
- •26.Векторно-координатный метод определения угла между прямой и плоскостью.
- •27.Векторно-координатный метод определения угла между двумя плоскостями
- •Алгоритм векторно-координатного метода:
- •Решение:
- •28.Векторно-координатный метод определения расстояния между фигурами.
- •29. Задачи на отыскание наибольшего и наименьшего значений геометрической величины.
- •30.Цилиндр. Решение задач на нахождение элементов цилиндра.
- •31.Конус. Решение задач на нахождение элементов конуса.
- •32.Усеченный конус. Решение задач на нахождение элементов конуса
- •33.Шар и сфера. Решение задач на нахождение элементов шара и сферы.
- •34. Части сферы и шара. Решение задач на нахождение элементов частей сферы и шара.
- •35.Комбинация шара с цилиндром.
- •36.Комбинация шара с конусом и усеченным конусом.
- •37.Комбинация конуса и усеченного конуса.
- •38.Взаимное расположение двух сфер.
- •43.Описанные многогранники.
- •44.Вписанные многогранники.
23. Применение векторов к решению аффинных задач в пространстве.
24.Применение векторов к решению метрических задач в пространстве.


25.Векторно-координатный метод определения угла между прямыми.

b




a





 AOB
AOB
Алгоритм векторно-координатного метода:
1). Введём прямоугольную систему координат и единицу измерения
2). Найдём координаты нужных точек
3).Найдём координаты направляющих векторов скрещивающихся прямых
4). Найдём угол между векторами
Задача.
В
кубе АВСD точки E и F середины рёбер соответственно
точки E и F середины рёбер соответственно
 и
и
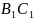 .
Найдите косинус угла между прямыми АЕ
и ВF
.
Найдите косинус угла между прямыми АЕ
и ВF
z
C



A
F
K

 – куб
– куб
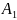
E
D
B
A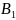
Найти:

y
x
1) Введём прямоугольную систему координат, как показано на рисунке
2) Общность задачи не нарушится, если ребро куба обозначить за 2
3) Найдём координаты нужных точек
А(2;0;0)
Е(2;1;2)
F(1;2;2)
B(2;2;0)
4) Введём направляющие векторы прямых АЕ и BF, и найдём их координаты:
 (0;1;2)
(0;1;2)
 (-1;0;2)
5)
Для нахождения косинуса угла между
прямыми воспользуемся формулой:
(-1;0;2)
5)
Для нахождения косинуса угла между
прямыми воспользуемся формулой:

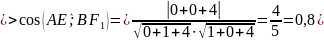 Ответ:
Ответ:

26.Векторно-координатный метод определения угла между прямой и плоскостью.
В

А
АВ =0, АВ
=0, АВ







 =
=
О


В
А


 =
=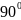
А
В


 =
=
Алгоритм векторно-координатного метода:
1). Используя особенности заданной фигуры ввести в пространстве прямоугольную систему координат
2).
Ввести
направляющий вектор прямой
 и найти его координаты
и найти его координаты
3).
Ввести
нормальный вектор плоскости
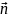 и найти его координаты
и найти его координаты
4).
Найти



