
- •1. Обобщенные приемы познавательной деятельности процесса поиска решения задач: функциональный подход.
- •2. Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов на плоскости
- •3. Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов в пространстве
- •Установление области определения.
- •Установление области изменения при заданной области определения.
- •Установление способа движения по множеству значений, при указанном способе движения по области определения.
- •Обобщенные приемы познавательной деятельности процесса поиска решения задач: аналогия, обобщение, конкретизация.
- •5. Обобщенные приемы познавательной деятельности процесса поиска решения задач: Метод математической индукции
- •6 . Обобщенные приемы познавательной деятельности процесса поиска решения задач: использование классических неравенств.
- •7.Функциональный подход в поиске решений задач: использование монотонности.
- •8.Функциональный подход в поиске решений задач: ограниченность (метод крайнего).
- •9.Функциональный подход в поиске решений задач: четности.
- •10.Функциональный подход в поиске решений задач: решение задач, содержащих целую и дробную часть числа.
- •Виды задач
- •Методы решения
- •12. Олимпиадные задачи. Основы теории чисел: простые числа, алгоритм Евклида.
- •13.Олимпиадные задачи. Инварианты. Полуинварианты.
- •14. Олимпиадные задачи, решаемые с использованием принципа Дирихле.
- •15. Комбинаторные задачи, приемы и методы их решения
- •16. Задачи на раскраски, укладки, замощения.
- •17. Диофантовы уравнения.
- •18. Логические задачи, решаемые с помощью графов
- •19. Логические задачи, решаемые с помощью составления таблиц истинности.
- •20. Олимпиадные задачи с геометрическим содержанием
- •21. Задачи - игры
- •22. Олимпиадные задачи с параметрами. Методы их решения.
- •23. Применение векторов к решению аффинных задач в пространстве.
- •24.Применение векторов к решению метрических задач в пространстве.
- •25.Векторно-координатный метод определения угла между прямыми.
- •Алгоритм векторно-координатного метода:
- •26.Векторно-координатный метод определения угла между прямой и плоскостью.
- •27.Векторно-координатный метод определения угла между двумя плоскостями
- •Алгоритм векторно-координатного метода:
- •Решение:
- •28.Векторно-координатный метод определения расстояния между фигурами.
- •29. Задачи на отыскание наибольшего и наименьшего значений геометрической величины.
- •30.Цилиндр. Решение задач на нахождение элементов цилиндра.
- •31.Конус. Решение задач на нахождение элементов конуса.
- •32.Усеченный конус. Решение задач на нахождение элементов конуса
- •33.Шар и сфера. Решение задач на нахождение элементов шара и сферы.
- •34. Части сферы и шара. Решение задач на нахождение элементов частей сферы и шара.
- •35.Комбинация шара с цилиндром.
- •36.Комбинация шара с конусом и усеченным конусом.
- •37.Комбинация конуса и усеченного конуса.
- •38.Взаимное расположение двух сфер.
- •43.Описанные многогранники.
- •44.Вписанные многогранники.
34. Части сферы и шара. Решение задач на нахождение элементов частей сферы и шара.
Ш аровым
сегментом
называется
часть шара, отсеченная от него плоскостью.
Если OP – радиус шара, перпендикулярый
отсекающей плоскости, то точку P назовем
в этом случае полюсом шара. Высотой
шарового сегмента называется отрезок
PO1,
соединяющий полюс шара с центром
основания шарового сегмента.
аровым
сегментом
называется
часть шара, отсеченная от него плоскостью.
Если OP – радиус шара, перпендикулярый
отсекающей плоскости, то точку P назовем
в этом случае полюсом шара. Высотой
шарового сегмента называется отрезок
PO1,
соединяющий полюс шара с центром
основания шарового сегмента.
Шаровой сегмент можно рассматривать как тело, образованное вращением кругового сегмента вокруг диаметра, перпендикулярного его хорде. Формулу объема шарового сегмента выводят так же, как и формулу объема шара, но интегрируют на промежутке (0; H) (H – высота шарового сегмента):
|

Шаровым сектором называется тело, образованное вращением кругового сектора вокруг оси, содержащей один из его граничных радиусов.
Шаровой сектор состоит из шарового сегмента и конуса. Поэтому его объем является суммой объемов шарового сегмента V1 и конуса V2:
35.Комбинация шара с цилиндром.

36.Комбинация шара с конусом и усеченным конусом.


37.Комбинация конуса и усеченного конуса.
Следует объяснить учащимся, что при решении различных задач на комбинацию конуса и усеченного конуса достаточно изобразить их сечение плоскостью, проходящей через ось конуса. В таком случае решение стереометрической задачи сводится к решению задачи планиметрической на комбинацию трапеции и треугольника.
Задача 1. Трапеция со сторонами 2, 2, 2 и 4 вращается вокруг прямой, лежащей в плоскости трапеции и проходящей через одну из вершин большего основания перпендикулярно этому основанию. Найдите объем тела вращения.
Решение. Пусть трапеция ABCD, у которой AB = BC = CD = 2, AD = 4, вращается вокруг прямой m, проходящей через вершину D перпендикулярно основанию AD. На рисунке 1 изображено осевое сечение полученного тела вращения (плоскость сечения проходит через ось вращения m). Это сечение состоит из двух равных и симметричных относительно прямой m трапеций ABCD и PMKD, которые равными прямоугольными треугольниками COD и KOD (O = m ∩ BC) дополняются до равных прямоугольных трапеций ABOD и PMOD. Это означает, что объем тела, полученного при вращении трапеции ABCD, равен разности объема усеченного конуса, полученного при вращении прямоугольной трапеции ABODвокруг прямой m, и объема конуса, полученного при вращении прямоугольного треугольника COD вокруг прямой m. Найдем объем тела вращения.

Высота конусов равна OD. Отрезки BO = r и AD = R являются радиусами соответственно верхнего и нижнего оснований усеченного конуса, а отрезок OC — радиус основания прямого кругового конуса с вершиной D. Найдем объемы этих конусов.
Проведем
отрезок BT параллельно CD.
Тогда из равенств BT = CD = AB = BC и BC = TDследует,
что AB = BT = AT,
откуда треугольник ABT —
правильный, в котором ![]()
При этом BM = 3BC = 6 (CK = AT = BC), значит,
![]()
(OD — серединный перпендикуляр BM). Тогда

и
искомый объем тела вращения равен
![]()
Ответ: ![]() куб. ед.
куб. ед.
38.Взаимное расположение двух сфер.
Возможны следующие случаи взаимного расположения двух различных сфер в пространстве:
1. Сферы не имеют ни одной общей точки, причем одна из них расположена вне другой. Необходимое и достаточное условие: сумма радиусов меньше расстояния между центрами сфер.
2. Сферы не имеют ни одной общей точки, причем одна из них расположена внутри другой. Необходимое и достаточное условие: модуль разности радиусов больше расстояния между центрами сфер.
3. Сферы пересекаются (имеют более одной общей точки). Необходимое и достаточное условие: расстояние между центрами меньше суммы радиусов, но больше модуля их разности. Пересечение двух сфер есть окружность.
4. Сферы касаются внешним образом (т.е. имеют общую точку и общую касательную плоскость в этой точке, причем центры сфер расположены по разные стороны от этой плоскости). Необходимое и достаточное условие: сумма радиусов равна расстоянию между центрами сфер.
5. Сферы касаются внутренним образом (т.е., имеют общую точку и общую касательную плоскость в этой точке, причем центры сфер расположены по одну сторону от этой плоскости). Необходимое и достаточное условие: модуль разности радиусов равен расстоянию между центрами сфер.
6. Сферы концентричны (т.е. их центры совпадают, а радиусы различны).
39.Комбинация цилиндра с многогранниками.

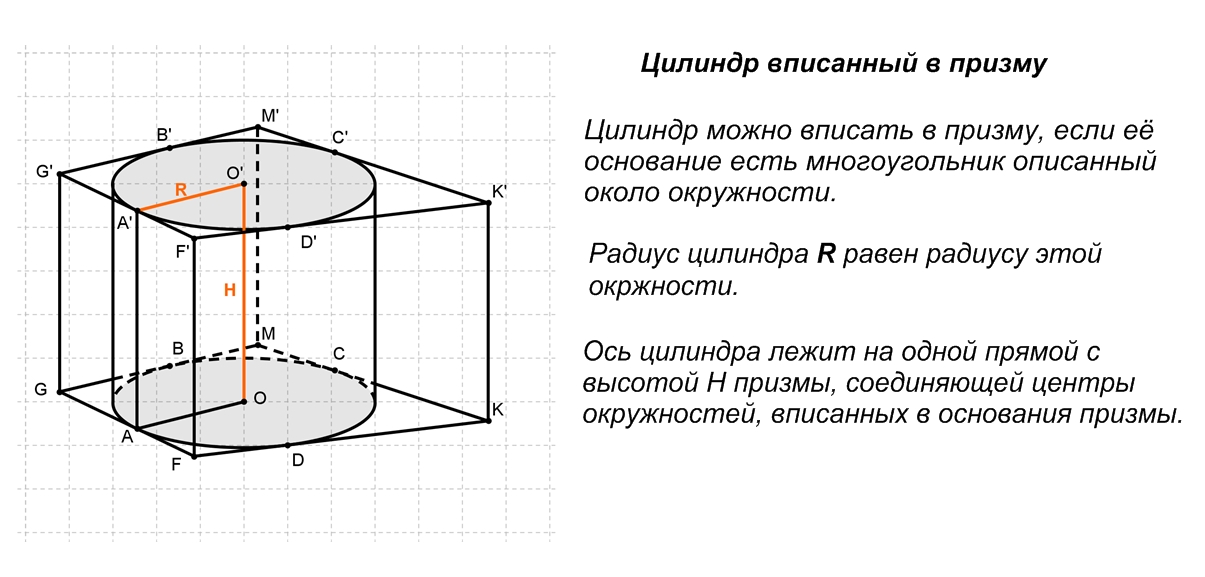

40.Комбинация конуса с многогранниками.

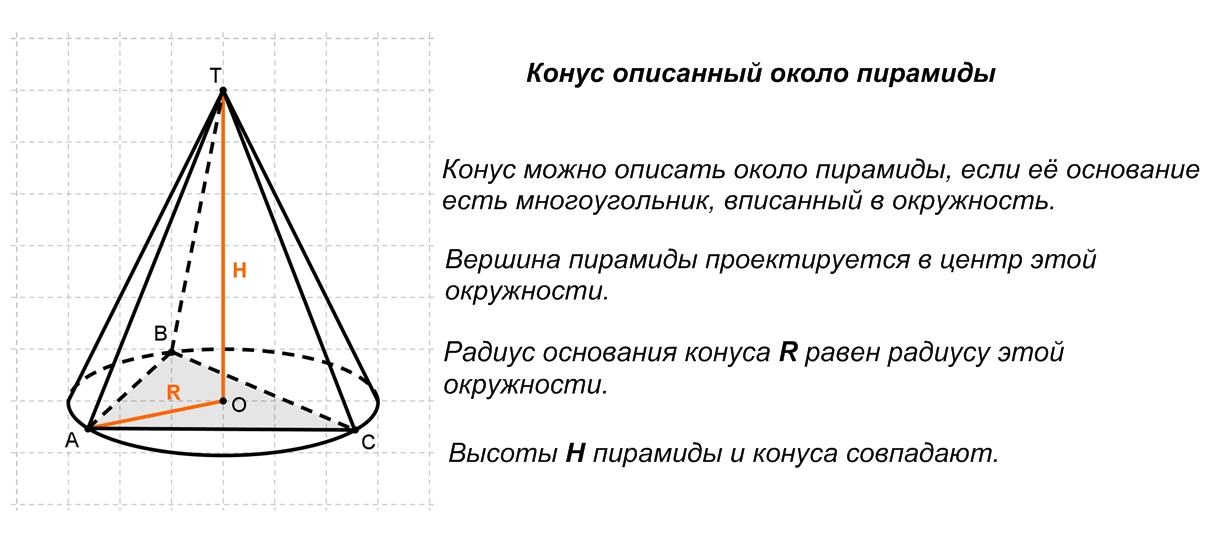

41.Комбинации усеченного конуса с многогранниками.
42.Комбинация шара с многогранниками.
1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
2. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника.
Теорема: В любую треугольную пирамиду можно вписать шар и притом единственный.
Доказательство:Пусть SABC – треугольная пирамида. Центр шара, вписанный в трехгранный угол с вершиной S, лежит на его пространственной биссектрисе L – геометрическом месте точек – центров всех сфер, касающихся граней трехгранного угла (l – есть пересечение биссекторных плоскостей двухгранных углов, образующих трехгранный угол). Центр шара, вписанного в двухгранный угол с ребром AB, лежит на его биссекторной плоскости α. L и α пересекаются в единственной точке O, которая одинаково удалена от всех граней пирамиды. Точка O – центр единственного шара, вписанного в пирамиду.
Следствие: Центр шара, вписанного в треугольную пирамиду – есть точка пересечения биссекторных плоскостей всех двугранных углов пирамиды.
Шар называется описанным около пирамиды, если все вершины пирамиды принадлежат шару.
Теорема: Через четыре точки общего положения можно провести сферу и притом единственную.
Доказательство:Пусть
S1A1B1C
– четыре точки общего положения, l
– прямая, перпендикулярная плоскости
ABC
и проходящая через центр ∆АВС,
α
– плоскость, перпендикулярная отрезку
SA
и проходящая через его середину. Тогда
 ,
O
– центр шара, проходящего через данные
четыре точки.
,
O
– центр шара, проходящего через данные
четыре точки.
Теорема:Если в пирамиду вписан шар, то его центр является точкой пересечения биссекторных плоскостей всех двугранных углов пирамиды.
Доказательство:Центр шара, вписанного в пирамиду, будучи равноудаленным от всех граней пирамиды, находится на каждой из биссекторных плоскостей двугранных углов пирамиды, т.е. является точкой пересечения всех биссекторных плоскостей.
Теорема: Если около пирамиды описан шар, то его центром является точка пересечения всех плоскостей, проведённых через середины рёбер пирамиды, перпендикулярно к этим рёбрам.
Доказательство:Известно, что множество точек, равноудалённых от двух вершин, является плоскость, проведённая через середину ребра перпендикулярно к нему. Поэтому центр шара, описанного около пирамиды, будучи равноудалённым от всех вершин пирамиды, находится на каждой из таких плоскостей, то есть является точкой их пересечения.
Замечание:Центр описанного около пирамиды шара лежит на перпендикуляре, проведённым через центр окружности, описанной около основания пирамиды.
Теорема: Около пирамиды можно описать сферу тогда и только тогда, когда её основание – многоугольник, около которого можно описать окружность.
Призма называется вписанной в шар, если все ее вершины лежат на поверхности шара. Основания призмы в данном случае вписаны в параллели шара, плоскости которых находятся на одинаковом расстоянии от центра.
Теорема:Для того чтобы около призмы можно было описать шар необходимо и достаточно, чтобы призма была прямой, и около ее оснований можно было описать окружности.
Замечание: Если около призмы описан шар, то его центр совпадает с серединой высоты призмы, проведенной через центры окружностей, описанных около оснований призмы.
Шар, в частности, можно описать около:
всякой прямой треугольной призмы;
всякого прямого параллелепипеда
всякой правильной n – угольной призмы.
Призма называется описанной около шара, если она касается его всеми своими гранями. Боковые грани призмы касаются шара в точках, расположенных на его экваторе.
Если призма описана около шара, то:
призма прямая;
высота призмы равна диаметру шара;
основания призмы – многоугольники, которые можно вписать в окружность.
