
- •1. Обобщенные приемы познавательной деятельности процесса поиска решения задач: функциональный подход.
- •2. Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов на плоскости
- •3. Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов в пространстве
- •Установление области определения.
- •Установление области изменения при заданной области определения.
- •Установление способа движения по множеству значений, при указанном способе движения по области определения.
- •Обобщенные приемы познавательной деятельности процесса поиска решения задач: аналогия, обобщение, конкретизация.
- •5. Обобщенные приемы познавательной деятельности процесса поиска решения задач: Метод математической индукции
- •6 . Обобщенные приемы познавательной деятельности процесса поиска решения задач: использование классических неравенств.
- •7.Функциональный подход в поиске решений задач: использование монотонности.
- •8.Функциональный подход в поиске решений задач: ограниченность (метод крайнего).
- •9.Функциональный подход в поиске решений задач: четности.
- •10.Функциональный подход в поиске решений задач: решение задач, содержащих целую и дробную часть числа.
- •Виды задач
- •Методы решения
- •12. Олимпиадные задачи. Основы теории чисел: простые числа, алгоритм Евклида.
- •13.Олимпиадные задачи. Инварианты. Полуинварианты.
- •14. Олимпиадные задачи, решаемые с использованием принципа Дирихле.
- •15. Комбинаторные задачи, приемы и методы их решения
- •16. Задачи на раскраски, укладки, замощения.
- •17. Диофантовы уравнения.
- •18. Логические задачи, решаемые с помощью графов
- •19. Логические задачи, решаемые с помощью составления таблиц истинности.
- •20. Олимпиадные задачи с геометрическим содержанием
- •21. Задачи - игры
- •22. Олимпиадные задачи с параметрами. Методы их решения.
- •23. Применение векторов к решению аффинных задач в пространстве.
- •24.Применение векторов к решению метрических задач в пространстве.
- •25.Векторно-координатный метод определения угла между прямыми.
- •Алгоритм векторно-координатного метода:
- •26.Векторно-координатный метод определения угла между прямой и плоскостью.
- •27.Векторно-координатный метод определения угла между двумя плоскостями
- •Алгоритм векторно-координатного метода:
- •Решение:
- •28.Векторно-координатный метод определения расстояния между фигурами.
- •29. Задачи на отыскание наибольшего и наименьшего значений геометрической величины.
- •30.Цилиндр. Решение задач на нахождение элементов цилиндра.
- •31.Конус. Решение задач на нахождение элементов конуса.
- •32.Усеченный конус. Решение задач на нахождение элементов конуса
- •33.Шар и сфера. Решение задач на нахождение элементов шара и сферы.
- •34. Части сферы и шара. Решение задач на нахождение элементов частей сферы и шара.
- •35.Комбинация шара с цилиндром.
- •36.Комбинация шара с конусом и усеченным конусом.
- •37.Комбинация конуса и усеченного конуса.
- •38.Взаимное расположение двух сфер.
- •43.Описанные многогранники.
- •44.Вписанные многогранники.
31.Конус. Решение задач на нахождение элементов конуса.
Прямым круговым конусом (или просто конусом) называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.
Фигура, полученная при вращении вокруг той же оси ломаной, составленной из гипотенузы и катета, не принадлежащего оси вращения, называется поверхностью конуса. Фигура, полученная от вращения гипотенузы, называется боковой поверхностью конуса, а фигура (круг), полученная от вращения катета, - основанием конуса (рис. 1).
Радиус этого круга называется радиусом основания цилиндра (на рис. 1 отрезок OA).
Катет
треугольника, принадлежащий оси,
называется высотой
конуса
(на рис. 1 отрезок SO - высота конуса).
Гипотенуза прямоугольного треугольника
называется образующей
конуса
(на рис. 1 отрезок AS - образующая
конуса).Р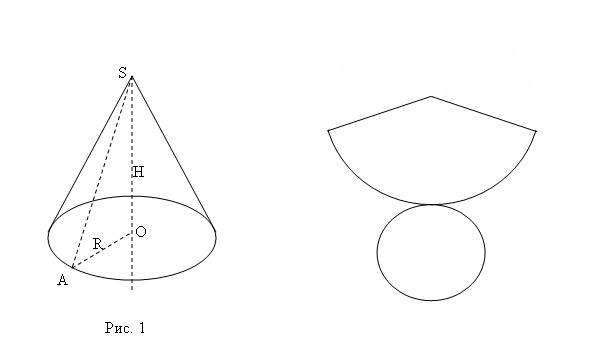 азвертка
боковой поверхности конуса является
круговым сектором, а полная развертка
поверхности конуса представляет собой
круговой сектор и круг (рис. 2).
азвертка
боковой поверхности конуса является
круговым сектором, а полная развертка
поверхности конуса представляет собой
круговой сектор и круг (рис. 2).
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник. Осевое сечение конуса – сечение, которое проходит через ось конуса. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность по окружности с центром на оси конуса.

Объем конуса вычисляется по формуле
Vкон= ,
где R - радиус основания конуса, H- высота
конуса.
,
где R - радиус основания конуса, H- высота
конуса.
Площадь боковой поверхности конуса вычисляется по формуле
Sбок=πRL, где R - радиус основания конуса, L - образующая конуса (L=∣AS∣ на рис. 1). Площадь полной поверхности конуса вычисляется по формуле
Sкон=
32.Усеченный конус. Решение задач на нахождение элементов конуса
Часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания, называется усеченным конусом.
Основания усеченного конуса - гомотетичные круги с центром гомотетии в вершине конуса (на рис. 3 в точке S). Усеченный конус можно получить в результате вращения равнобедренной тралении вокруг ее оси симметрии (на рис. 3 трапеции AA1B1B). При вращении границы этой трапеции получается поверхность усеченного конуса.
 Боковая
сторона трапеции называется образующей
усеченного конуса; круги, полученные
при вращении оснований трапеции, -
основаниями усеченного конуса.
Боковая
сторона трапеции называется образующей
усеченного конуса; круги, полученные
при вращении оснований трапеции, -
основаниями усеченного конуса.
Развертка усеченного конуса представляет собой объединение части кругового кольца и двух кругов (рис. 4).

Объем усеченного конуса вычисляется по формуле

где H - высота усеченного конуса, R1 и R2 - радиусы верхнего и нижнего оснований усеченного конуса.
Площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса вычисляется по формуле
 ,
где L - образующая усеченного конуса.
,
где L - образующая усеченного конуса.
33.Шар и сфера. Решение задач на нахождение элементов шара и сферы.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
Данная точка называется центром сферы, а данное расстояние - радиусом сферы.
Отрезок, соединяющий центр О сферы с любой ее точки М, также называется радиусом.
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется ее диаметром, а соответствующие концы диаметра называются диаметрально противоположными. Диаметр D сферы равен двум радиусам: D = 2R (см. рис. 62).
 Тело,
ограниченное сферой, называется шаром.
Центр, радиус, диаметр сферы являются
также центром, радиусом, диаметром шара.
Шар радиуса R с центром в точке О содержит
все точки пространства, которые
расположены от точки О на расстоянии
не больше, чем R. Сечения сферы (шара)
плоскостью являются окружностями
(кругами).
Тело,
ограниченное сферой, называется шаром.
Центр, радиус, диаметр сферы являются
также центром, радиусом, диаметром шара.
Шар радиуса R с центром в точке О содержит
все точки пространства, которые
расположены от точки О на расстоянии
не больше, чем R. Сечения сферы (шара)
плоскостью являются окружностями
(кругами).
Площадь сферы
![]()
Объем шара, ограниченного сферой
![]()

