7. Теорема о пределе ограниченной функции.

Теорема: если f(x) имеет конечный предел при x→aто эта f(x)

Док-во:Пусть lim_x→af(x)=Aто есть по определению предела

|f(x)-A+A|≤|f(x)-A|+|A|⇒|f(x)|<ε+|A|то есть

|f(x)|<M=ε+|A|⇒по определению ЧТД

18)Бесконечно малые функции и их свойства. Бесконечно большие функции и их связь с бесконечно малыми.

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Пример: f(x) - бесконечно малая функция если х->0;

F(X) – не бесконечно малая функция если х->1 и т.д;

Теорема {без док-ва}:

Для того, чтобы f(x) при x→a имела предел, необходимо и достаточно, чтобы вблизи точки х=a выполнялось , где - бесконечно малая при x->a;

Свойства бесконечно малых функций:

1. сумма фиксированного числа бесконечно малых функций будет бесконечно малой функцией при x->a;

2. если взять фиксированное число бесконечно малых функций, то их произведение – тоже бесконечно малая функция;

3. произведение бесконечно малой функции на ограниченную функцию будет бесконечно малой функцией;

4. деление бесконечно малой функции на ограниченную с будет бесконечно малой функцией;

Функция y=f(x) называется бесконечно большой если предел функции f(x) при x->a равен плюс-минус бесконечности или же просто бесконечности.

Связь бесконечно малых функций и бесконечно больших функций.

Если f(x)->0 и не обращается в 0, то т.е и наоборот.

19) Сравнение бесконечно малых функций. Свойства эквивалентных бесконечно малых функций.

Пусть - бесконечно малые функции при x->a; их можно сравнивать по быстроте убывания.

Если то - б.м. более высокого порядка, чем .

Если то и одного порядка малости, если А=1, то и - эквивалентные ( ~ );

Бесконечно малая функция называется порядка малости k относительно , если .

Не все бесконечно малые функции можно сравнивать между собой. Если или не существуют, то и - несравнимые.

Свойства эквивалентныхб.м.ф.:

1. функция эквивалентна сама себе;

2. ~ и ~ => ~ ;

3. ~ ; ~ ; ; => ;

4. ~ ; => ~ ;

20. Основные методы отыскания пределов. Замечательные пределы. Вывод.

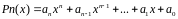
1. Qm(x)≠0 в точке а ⇒f(x)=p(x)/Q(x) –непрерывна в точке а и

2. Qm(x)=0; Pn(x)≠0 в точке а ⇒А=∞

3. Qm(а)=0; Pn(а)=0⇒

4. Qm(a)≠0; Pn(a)≠0 ⇒

так ка f(x) непрерывна⇒

⇒

∞ -∞=неопр ∞*0=неопр 1^∞=неопр

∞

L

+∞=∞ ∞/∞=неопр

Замечательные пределы:

1. 

   H

   K

   А

   

2. 

Вывод:

1)Soна<Sсек<Sola тН- пересечение луча и окружности

Sона=1/2*нк*оа*sinx=(sinx)/2 т К –проекция точки Н на ось Х

S сеч= ½*R²*x=x/2 т А (1,0)

Sola=1/2*La*oa*sinx=(tgx)/2 т L точка пересечения касательной и луча

2) 3)cosx<(sinx)/x<1 ⇒

т.к. х∈(0,п/2)⇒sinx>0 ; tgx>0