5) Множество вещественных чисел. Основные характеристики вещественных чисел: и соотношения между ними. Верхняя и нижняя грани множества действительных чисел.
Множество R = {a, b, c, ...} называется полем действительных (вещественных) чисел, если для его элементов установлены бинарные отношения и бинарные операции, подчиненные перечисленным ниже аксиомам.
Аксиомы сложения
элемент
с, называемый их суммой и обозначаемый
a+b.
При этом выполняются следующие аксиомы:
1. a+b=b+a (коммутативный закон);
2. (a + b) + c = a + (b + c) (ассоциативный закон);
3.
В R существует
элемент, называемый нулем и
обозначаемый символом 0, такой, что 
a +
0 = a.
4.
существует
такое число
,что
выполняется равенствоa+(-a)=0.
Таким образом, множество R является аддитивной абелевой группой.
Аксиомы умножения
действительное
число с, называемое их произведением и
обозначаемое
.
При этом выполняются следующие аксиомы:
1.
;
2. 
(ассоциативный
закон);
3.
В R существует
элемент, называемый единицей и
обозначаемый символом 1, такой,
что 
справедливо
равенствоa*1=a
4. 
существует
элемент 
,
называемый обратным числу a,
такой, чтоa*a-1=1
Следовательно, множество ненулевых элементов множества R является мультипликативной абелевой группой. Операция умножения дистрибутивна относительно сложения, т.е.a(b+c)=ab+ac ⩝a,b,c R
Аксиомы порядка
1. 
(рефлексивность).
2. 
(антисимметричность).
3. 
(транзитивность).
4. 
или 
,
или 
,
или то и другое.
Следующие две аксиомы связывают отношение порядка и бинарные операции:
1.
Если 
и
,
то 
.
2.
Из 
и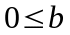 
следует 
.
Основные характеристики вещественных чисел.
Для действительного числа x введем следующие характеристики: |x| - модуль x, sgn x - знак x,x+ - положительная часть x и x- - отрицательная часть x. Они вводятся по правилам:
Очевидны
следующие соотношения между этими
характеристиками 
:
При решении задач часто применяются неравенства
Вместе
с указанными характеристиками полезно
также рассмотреть функции
.
Первая и вторая функции являются
мультипликативными отображениями,
поскольку из определения этих функций
следуют равенства:
Из
всех перечисленных характеристик
действительного числа наиболее важной
является его модуль. Под основными
свойствами модуля числа понимают
следующее:
1) 
;
2) 
;
3) 
.
Последнее
неравенство называется неравенством
треугольника,
поскольку оно имеет геометрический
смысл в случае, когда 
.
Аксиома о верхней (нижней) грани
Множество A
R называется ограниченным
сверху(снизу),
если существует элемент 
такой,
что 
(
)
,
при этом число M называется верхней
(нижней) гранью множества A.
Множество
A
R
называется ограниченным, если существует
такое,
что
выполнено
.
Всякое ограниченное сверху
множество A
R имеет
точную верхнюю грань.
Множество
А не ограничено, если для любой постоянной
найдется
число
такое,
что
>M.
Наименьшее
из чисел, ограничивающих множество А
сверху, называется точной верхней
гранью. Наибольшее из чисел, ограничивающих
множество А снизу, называется точной
нижней гранью. Обозначения:
-точная
верхняя грань
-точная
нижняя грань
На «языке» неравенств последнее определение записывается так:
Число
является
точной верхней (нижней) гранью множества,
если:
1)
выполнено
(
);
2)
такое, что
(
).