
- •1.Множества (пустое, универсальное, упорядоченное). Счетное множество. Примеры счетных и несчетных множеств.
- •2. Операции над множествами. Булева алгебра. Бинарные отношения и бинарные операции.
- •3.Функция. Отображение. Сюръективное, инъективное, биективное отображения. Суперпозиция отображений. Обратное отображение.
- •4) Комплексные числа. Определение, свойства, алгебраическая и тригонометрическая формы записи. Модель и аргумент комплексного числа.
- •5) Множество вещественных чисел. Основные характеристики вещественных чисел: и соотношения между ними. Верхняя и нижняя грани множества действительных чисел.
- •6.Теорема о существовании точной верхней/нижней грани.
- •Теорема о единственности точной верхней/нижней грани.
- •Числовая последовательность. Операции над последовательностями. Подпоследовательности. Свойства последовательностей. Предельная точка.
- •Виды последовательностей. Ограниченные, неограниченные, стационарные последовательности. Свойства ограниченных последовательностей.
- •Предел последовательности. Теоремы о единственности предела последовательности.
- •Теорема об ограниченности сходимой последовательности.
- •Теорема Больцано - Вейерштрасса.
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Число е, как предел последовательности. Связь натурального и десятичного логарифмов.
- •Бесконечно малые и бесконечно большие последовательности. Свойства.
- •Предел функции в точке и на бесконечности. Односторонние пределы (определения Коши, Гейне). Основные свойства пределов числовых функций.
- •Теорема о пределе ограниченной функции.
- •18)Бесконечно малые функции и их свойства. Бесконечно большие функции и их связь с бесконечно малыми.
- •19) Сравнение бесконечно малых функций. Свойства эквивалентных бесконечно малых функций.
- •21. Понятие непрерывности в точке и на множестве. Свойства непрерывных функций. Классификация точек разрыва.
- •Теорема Вейерштрасса (об ограниченности непрерывной функции)
- •23) Теорема о промежуточных значениях непрерывной функции
- •24) Критерий непрерывности монотонной функции (Теорема)
- •25. Непрерывность обратной функции. Теорема о существовании обратной функции у монотонной.
- •27. Дифференцирование функции. Производная функции. Определение, геометрический смысл, основные правила дифференцирования. Односторонние производные.
- •Производные основных элементарных функций (вывод).
- •29) Теорема о производной сложной функции.
- •30) Теорема о производной обратной функции.
- •Логарифмическое дифференцирование. Производная показательно-степенной функции.
- •Дифференциал функции, его геометрический смысл и основные свойства.
- •Дифференциал сложной функции. Инвариантная форма записи дифференциала
- •Формула Тейлора (доказательство).
- •Основные теоремы о производных. Теорема Ролля. Теорема Логранжа. Теорема Коши.
- •Теорема (правило) Лопиталя.
- •Производные и дифференциалы высших порядков. Формула Лейбница.
- •Исследование функции с помощью производной. Теорема о возрастании и убывании функций. Критические точки. Точки экстремума.
- •Теорема (необходимое условие существования экстремума).
- •Теорема (достаточные условия существования экстремума).
- •Нахождение наибольшего и наименьшего значений функции на отрезке.
- •Исследование функции на экстремум с помощью производных высших порядков. Теорема о существовании максимума/ минимума функции.
- •Выпуклость и вогнутость кривой. Теорема (о знаке второй производной).
- •44. Точки перегиба. Теорема о точке перегиба.
- •49. Интегрирование элементарных дробей.
- •50. Интегрирование рациональных функций.
- •51. Интегрирование тригонометрических функций.
3.Функция. Отображение. Сюръективное, инъективное, биективное отображения. Суперпозиция отображений. Обратное отображение.
Отображением множества E в
множество F,
или функцией,
определенной на E со
значениями в F,
называется правило, или закон f,
который каждому элементу x
E ставит
в соответствие определенный элемент
f(x)
F .
Элемент x
E называют независимым
элементом,
или аргументом функции f,
элемент f(x)
F называют значением
функции f,
или образом;
при этом элемент x
E называется
прообразом элемента f(x)
F .
Отображение (функцию) обычно обозначают
буквой f или
символом f:
E ,
указывая тем самым, что f отображает
множество E в F.
Употребляется также обозначение x
,
указывая тем самым, что f отображает
множество E в F.
Употребляется также обозначение x ,
указывающее, что элементу x соответствует
элемент f(x).
,
указывающее, что элементу x соответствует
элемент f(x).
Отображение
f:
E называется:
называется:
- инъективным (или инъекцией,
или взаимно
однозначным отображением множества E
в F),
если
 ,
или
,
или
 если уравнение f(x)
= y имеет
не более одного решения;
если уравнение f(x)
= y имеет
не более одного решения;
- сюръективным (или сюръекцией, или отображением множества E на F), если f(E)= F и если уравнение f(x) = y имеет по крайней мере одно решение;
- биективным (или биекцией,
или взаимно
однозначным отображением множества E на
F),
если оно инъективно и сюръективно, или
 если уравнение f(x)
= y имеет
одно и только одно решение.
если уравнение f(x)
= y имеет
одно и только одно решение.
Пусть
f:E
и
 .
Поскольку
.
Поскольку
 ,
то отображение g каждому
элементу f(x)
f (E)
,
то отображение g каждому
элементу f(x)
f (E)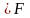 относит
определенный элемент
относит
определенный элемент  .
Таким образом, каждому
.
Таким образом, каждому  посредством
правила
посредством
правила  поставлен
в соответствие элемент
поставлен
в соответствие элемент
 .
.
Тем самым определено новое отображение (или новая функция), которое назовем композицией отображений, или суперпозицией отображений, или сложным отображением.
Пусть f:E
-
биективное отображение и F ={y}.
В силу биективности f каждому  соответствует
единичный образ x,
который обозначим через f -1(y),
и такой, что f(x)
= y.
Таким образом, определено отображение
соответствует
единичный образ x,
который обозначим через f -1(y),
и такой, что f(x)
= y.
Таким образом, определено отображение
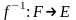 ,
которое называется обратным
отображению f,
или обратной
функцией функции f.
Очевидно, отображение f обратно
отображению f -1.
Поэтому отображения f и f
-1 называют
взаимно
обратными.
Для них справедливы соотношения
,
которое называется обратным
отображению f,
или обратной
функцией функции f.
Очевидно, отображение f обратно
отображению f -1.
Поэтому отображения f и f
-1 называют
взаимно
обратными.
Для них справедливы соотношения




- инъективным (или инъекцией, или взаимно однозначным отображением множества E в F), если , или если уравнение f(x) = y имеет не более одного решения;
- сюръективным (или сюръекцией, или отображением множества E на F), если f(E)= F и если уравнение f(x) = y имеет по крайней мере одно решение;
- биективным (или биекцией, или взаимно однозначным отображением множества E на F), если оно инъективно и сюръективно, или если уравнение f(x) = y имеет одно и только одно решение.
4) Комплексные числа. Определение, свойства, алгебраическая и тригонометрическая формы записи. Модель и аргумент комплексного числа.
Комплексные числа
Комплексным
числом z
называется
выражение
 ,
где a
и b
– действительные числа, i
– мнимая единица, которая определяется
соотношением:
,
где a
и b
– действительные числа, i
– мнимая единица, которая определяется
соотношением:

При этом число a называется действительной частью числа z (a = Rez), а b- мнимой частью (b = Imz).
Если a =Rez =0, то число z будет чисто мнимым, если b = Imz = 0, то число z будет действительным.
Свойства:
1.
 ;
;
2.
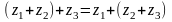 ;
;
3.
можно
определить противоположный элемент
 ,
который обладает следующим свойством
,
который обладает следующим свойством
 ;
;
4.
обозначим  =
(0, 0), тогда для любого z
будет выполнено z +
=
z;
=
(0, 0), тогда для любого z
будет выполнено z +
=
z;
5.
 ;
;
6.
 ;
;
7.
определим  =(1,0)
, тогда
=(1,0)
, тогда  ;
;
8. (обратный
элемент):
(обратный
элемент):
 ;
;
9.
 ;
;
10.
 ;
;
Алгебраическая форма записи:
Запись комплексного числа z в виде x+iy; x,y R , называется алгебраической формой комплексного числа.
Тригонометрическая форма записи:
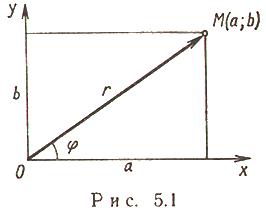
Если вещественную x и мнимую y части комплексного числа выразить через модуль r=|z| и аргумент ф(x=rcosф, y=rsinф), то комплексное число z можно записать в тригонометрической форме:
z=r(cosф+isinф).
Модель и аргумент комплексного числа:
Ф= argz, (-п<ф<=п либо 0<=ф<2п ) - аргумент комплексного числа z (главное значение аргумента);
Arg z - множество аргументов числа z:
argz= argz+ 2 пк, к z
ФормулаЭйлера:


