§16. Сравнение роста стнпенной логарифмич. И показатю функции.

В §21 I ч. мы сравнивали беск. малые и беск. большие ф-ции. Рассмотрим част. случай, когда при ф-ции f(x) и g(x) явл. беск. большими, т.е. неогр. возрастают при , тогда если , то говорили, что в числителе б.б.ф. более высок. порядка, чем в знаменателе, а если этот предел был равен 0, то в знаменателе выше порядок, чем в числителе. Если же предел их отношения равен конечному, отличному от нуля числу, то эти беск. больш. одинак. порядка, т.е. одинаковый рост стремления при .

Рассмотрим случай:

1. пусть .

а) - некоторое натур. число, тогда

. След-но показ. ф-ция е^х растет быстрее степенной ф-ции х , где - натур.

б) пусть - любое веществ. число, по положит-е, тогда используя ф-цию от легко док-ть тоже утверждение, что и при - натур., т.к.

2. Пусть теперь

, т.е. в числителе получаем беск. больш. ф-цию со скоростью стремления к бесконечности низшего порядка, чем в знаменателе. .

Аналогично, рассматривается случай ф-ций а^х и log_ax, если а>1.

Вывод: таким обр., мы получили, что из 3х рассм-х ф-ций: показат., степ. и логариф. при . медленнее всех стремится к бесконечности логарифмич. ф-ция, а быстрее всех показат. ф-ция.

Применение диф. исчесления.

Раздел 4. Иссл-е ф-ций методом диф. Исчисления и постр-е графиков.

§17. Условия постоянства возр-я и убывания ф-ции.

Теорема 1: пусть на отрезке [a;в] определена непр. ф-ция f(x) и диф-ма внутри него.

Тогда: 1) для того, чтобы f(x) была постоянной на [a;в] необх. и дост., чтобы f^\(x) была равна 0 на интервале (а;в).

2) Для того, чтобы f(x) была возрастающей (убыв.) на [a;в] необх. и дост., чтобы на интервале (a;в) .

3) Для того, чтобы ф-ция f(x) была строго возрастающей (стр. убыв.) на отрезке [a;в] дост, чтобы на интервале (а;в) вып-сь .

Д-во: 1. Необходимость.

Т.к. известно, что производная от пост. ф-ции =0, то необх-ть сразу вытекает из усл-я.

Дост. пусть f(x) непр. на отр. [a;в] и диф. внутри него, тогда можно применить т. Ллагранжа, т. е. ф-лу конеч. приращений на отрезке [a;x], где х – любая точка из отрезка [a;в]. В рез-те получим ф-лу Лагранжа Т.к. по условию , то справа получаем 0, а след-но f(x)=f(a) для , а след-но, f(x)=const на отрезке [a;в].

2. Д-жем теперь 2-ой случай, причем для возраст. ф-ции, т.к. для убывающ. док-ся аналогично.

Необх. : пусть f(x) – монотонно возрастает. (самост.)

§18. Экстремум ф-ции. Наиб. И наим. Знач-я.

Опр. Ф-ция f(x), заданная на некотор. внутр. точке х₀, если в некотор. проколотой окр-ти выполняется нер-во: . Максимум или мин. принято наз. экстремум (от лат. - крайний).

Макс. или мин. ф-ции во внутр. т. х₀ иногда наз. локальный экстремум (в пер. – в некотор. окр-ти точки). Лок. экстр., т.е. max и min ф-ции в некотор. окр-ти точки нельзя смешивать с наиб. или наим. знач-ем ф-ции f(x) на заданном промежутке. Наиб. или наим. знач-я ф-ции принято наз. глобальным экстремумом.

Чтобы найти точки экстрем. ф-ции определили необх. и дост. условия и существования экстремума.

Пусть ф-ция f(x) определена на отрезке [a;в] и в некотор. точке она имеет экстремум. Это значит, в некотор. окр-ти т. х₀, ф-ция принимает или наиб. или наим. знач-я, по опр-ю. Тогда, если в этой т. х_0­ производная, то т. Ферма . Таким образом, необх. условием существования экстремума в точках, где существует конечная производная явл-ся рав-во 0 производной.

След-но, чтобы найти точки, в которых производная =0, дост. решить ур-ние . Найдя корни этого ур-ния, мы получим точки, в которых может быть экстремум. Среди которой ур-ние могут быть точки, в котор. не экстремум, а это значит, что равенство о производной не явл. дост. усл-ем для существования экстремума.

y=x³;

Опр. Точки, в котор. произ. равн0 0, наз. стационарными.

Кроме стацион. точек подозрительными точками на экстр. явл. точки, в котор. либо =∞ производная, либо вовсе несуществует.

y=|x|

Все, подозрит. точки на экстремум, принято наз. критич. точками. Укажите 2 способа исследования критич. точек на экстремум (локальный).

1. Пусть т. х₀ явл. критической, т.е. в некотор. окр-ти т. х₀ : за исключением быть может самой точки х₀ производная , котор. на промежутках имеет постоянный знак, тогда возможна след. случай:

а) .

Используя теорему §17. мы заключаем, что ф-ция f(x) при х<x₀ убывает, а при x>x₀ – возрастает, а это значит, что в т. х₀ ф-ция принимает наим. знач-е из рассматриваемой окр-ти, т.е. f(x₀) – минимум.

б) .

Рассуждая аналогично, получаем, что слева от т.х₀ ф. /, а справа \, а это значит, что f(x₀) есть max.

3) . А это значит, что в т. х₀ ф-ция не имеет наиб. или наим. значений в рассматриваемой окр-ти, т.е. ни емеет ни максимума ни минимума.

Таким образом,если произ-ная ф-ции при переходе ч/з критич. точку х₀ меняет знак, то в этой точке ф-ция имеет экстремум. Причем, если меняет с – на +, то min, если с +на - -max. Это усл-е явл. достаточным для существования экстремума ф-ции f(x) в критич. точке:

Замечание: если ф-ция имеет несколько крит. точек в обл. её определения, а м/д крит. точками производная непрерывна, то все крит. точки необходимо распложить впорядке возрастания , где отрезок (a;в] – обл. опр. ф-ции. В кажд. из получ. интервалов (а₁х₁),(а₁х₂)…(х_n;в) существует производная .

Кроме того, на кажд. из получ. интервалов имеет постоян. знак. для опред-я знака достаточно выбрать побную точку из каждого интервала, тогда получим некотор. посл-ть хнаков , что позволит сразу решить вопрос об экстрем. ф-ции в кажд. крит. точке. Знак произ-ной по кажд. интервале указывает на монотонность ф-ции в них.

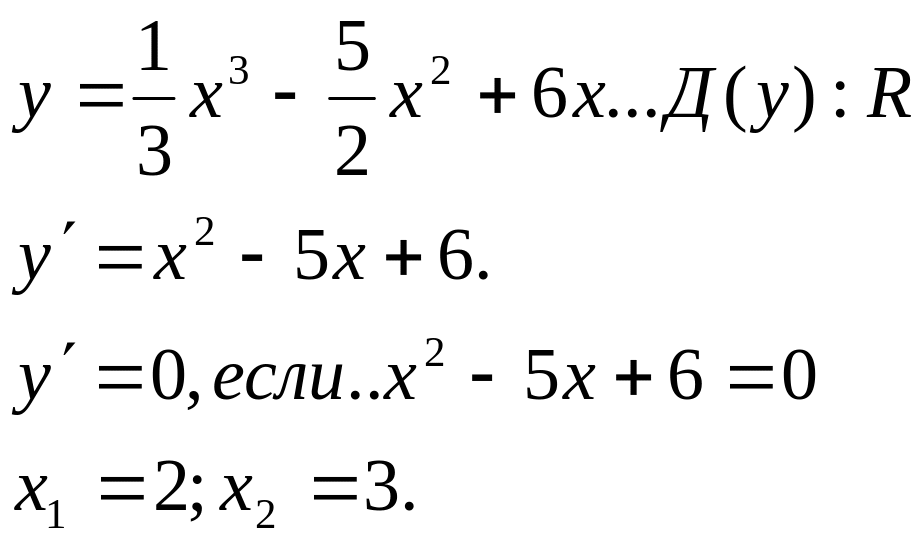
x	(-∞;2)	2	(2;3)	3	(3;+∞)
y\	+	0	-	0	+
y		max		min

2. Пусть ф-ция f(x), заданная на интервале (a;в) имеет крит. точку х₀, в котор. первая конечн. производная, а, след-но, . Предположим, что в этой точке 2-ая производная . Тогда, если , то в точке х₀ ф-ция имеет max, а если , то min. Д-жем это утверждение. По определению второй производной имеем:

.

Используя св-во 2 §17 ч I, заключаем, что вблизи т. х₀ знак совпадает со знаком выражения . След-но, рассматривая значение х, вблизи т. х₀, получим 2 случая:

1). а это значит, что числитель и знаменатель имеет одинак. знак, т.е. если , если . По I правилу это означает, что f(x₀)-min.

2)

а это значит, что f(x₀) – max.

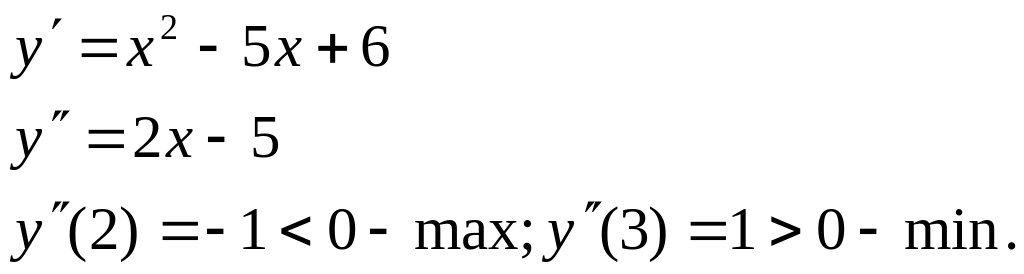
Замеч. Сравнивая 1и 2 способ иссл-я ф-ции заключаем, что 2 способ практически более удобный. Однако он не всегда применим. Когда 1-ая производная =∞ или несуществует, а также когда , то 2-ое правило не пременимо, поэтому применяем 1-ое правило.

Наиб. и наим. знач-я ф-ции на заданном отрезке.

Пусть ф-ция y=f(x) задана на [a;в] и пусть на нем непрерывна. Тогда по теореме Вейерштраса на заданном отрезке ф-ция f(x) достигает своего наиб. и наим. значений. Возможны 2 случая : 1) наиб. или наим. знач-е достигается во внутр. точке[a;в]. В этом случае max ф-ции или min ф-ции явл. локальным экстремумом: 2) наиб. или наим. знач-е достигается на конце [a;в], тогда оно не может быть локальным экстремумом.

Для того, чтобы найти наиб. или наим. знач-е ф-ции f(x) на [a;в], нужно:

1. Найти производную данной ф-ции;

2. Вычислить все крит. точки ф-ции;

3. Вычислить значения ф-ции в кажд. крит. точке.

4. Выбрать из всех полученных знач-ий ф-ции наиб. или соответственно наим.

Естественно, здесь предпологается, что мн-во крит. точек-конечное.