§3. Геометрич. И физический смысл производной и дифференциала функции.

В конце XVII в. велик. матем. и физик И. Ньютон построил модель мех. движ-я, он показал связь м/д путем и скоростью, что стало проводным пунктом в истории естествозн-я.

Если МТ движ-ся прямолинейно заданной вдоль некоторой прямой, то скорость прямолин. движ-я этой точки явл. производной координаты (пути) х₊ по времени t. .

Ф-ция S=x(t) наз. законом движ-я точки. Г. Лейбниц, решая задачу проведения касательной к произвольной кривой, пришел к понятию производной иным путем и показал: геометр. смысл производной состоит в том, что значение произ. ф. в точке = угл. коэф. касат., проведенной к граф. ф-ции в этой точке, т.е. f^/(x)=tg . На интерпретации производной как скорости изм-я одной величины относит. другой все физ. явл-я на применении производной.

Применение дифференциала ф-ции основано на том, что приращение ф-ции заменяется её дифференциалом, что позволяет заменить любую диф. в точке х₀.

Рассм. некотор. ф-цию y=f(x) заданную в некотор. окр-ти т. х₀: .Её графиком явл. некотор. кривая на коор. пл-ти ХОУ. Пусть эта ф-ция будет непрерывна в задан. окр-ти. Дадим некотор. приращение и такое , что , в котор. ф-ция задана.

На кривой y=f(x) рассмотрим точки М(х₀;f(x₀)) и .

Проведем прямую, проходящую ч/з точки N и М, назовёи её секущей МN к оси ОХ ч/з , тогда очевидно зависит от !

Опр. Если сущ. предельное полож-е секущей MN при стремлении точки N граф. ф-ции к т. М, когда , то это пред. полож-е наз. касательной, проведенной к графику ф-ции f в т. М(х₀;f(x₀)). Это значит, что .

Теорема. Если ф-ция y=f(x) имеет в данной точке х₀ производную, то касательная.проведенная к графику ф-ции. f в точке М(x₀;f(x₀)), причем угл. коэф. этой касательной : . Угл. коэф. касат. – это tg угла наклона её к оси ОХ.

Д-во т. сразу следует из рассмот-я .

. Переходя к пределу при , получаем

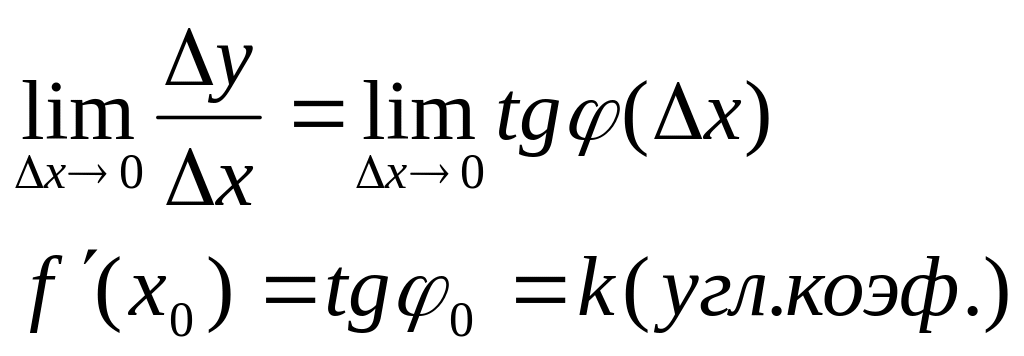
Ч.т.д.

Используя определении дифференциала ф-ции в т. х₀, можем получить геометр. интерпретацию дифференциала ф-ции. Рассмотрим , где МК- касательная, тогда получим .

Таким образом получаем, что если - приращение ординаты кривой y=f(x), то дифференциал dy явл. приращением ординаты касательной. В этом и состоит геом. смысл дифференциала ф-ции в задан. точке.

Если же предел при , то это означает, что касат., проведенная к графику ф-ции к. т. М(х₀;f(x₀)) оси ОХ.

§5. Дифференцирование сложной функции.

Теорема. Пусть заданы ф-ции в некот. окр-ти . Если ф-ция, являющаяся композицией этих 2х ф-ций: задана в нектор. окр-ти т. х₀ из окр-ти , то слож. ф-ция F(x) диф в точке х₀, причем справедливо рав-во : или .

Д-во: дадим приращение точке х₀ , равное , оно вызовет приращение ф-ции, равное , причем . Приращение вызывает приращение ф-ции . По условию ф-ция t=f(x) диф. в т. х₀ , поэтому по опр-ю диффер-ти ф. в точке, получим , где А – число, . Ф-ция диф. в т. t₀ её приращ. (3), где В-число, . Подставляя (2) в (3) получаем . АВ-число; по построению.

В силу дифференцируемости ф-ции t=f(x) следует её непрерывность (т.2 §2), а по определению 5 §22 это означает, что , след-но, при , а значит и , поэтому сумма, стоящ. в скобках, которую обозначим . Таким образом, мы получили, , где АВ- число, не завис. от , а . Это значит, что ф-ция y=F(x) диф. в т. х₀.

Из последнего равенства сразу получаем рав-во (1), т.е. правило диф-я слож. ф-ция производная слож. ф-ции по независ. переменной = произв-ю производной ф-ции по промежуточному аргументу на производную промежуточного аргумента по незав. переменной: .

Эта т. справедлива для композиции более 2х ф-ций, обязат-но диф-мых.